因网页不支持数学公式,所有试题请以图片为准。
本人是一名数学教师,也是一名公益志愿者。
如果我的付出,对你或你的亲友有所帮助,期待你
(1)关注我!
(2)在评论区留言支持!
(3)把这份资料转发给需要它的同学!
(4)你自己(亲友)能收藏用上这份资料!
(5)在本文之前和之后,已发布大量的相关复习资料,欢迎查阅使用。

菱形的定义是建立在平行四边形基础上的,它指平面内,有一组邻边相等的平行四边形。
与矩形类似,菱形也是平行四边形,具有所有平行四边形的性质。同时,菱形相比较平行四边形而言,有一组菱边相等,所以菱形又具有一些特殊的性质:比如菱形的四条边都相等;菱形的对角线互相垂直;菱形的每一条对角线都平分一组对角;菱形也是轴对称图形,菱形的对称轴有2条,即两条对角线所在直线;菱形还是中心对称图形,对称中心是两条对角线交点。
菱形的判定主要是基本菱形的定义和菱形的特殊性质进行研究后得到的。其主要内容分别是:一组邻边相等的平行四边形是菱形;四边相等的四边形是菱形;对角线互相垂直的平行四边形是菱形;对角线互相垂直平分的四边形是菱形。
与菱形有关的计算公式主要有:面积公式,S=边长×高=两对角线积的一半;周长公式,C=边长的4倍。
本单元考题的主要特点就是难度大,综合性强。所涉及的知识面广,方法灵活多样。我们以第2题为例看一看:
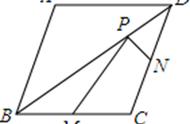
此题是一个综合性比较强的题目,其解题的思路为: ①先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;
②证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积;
③过点F作FP∥AE于P点,根据题意有FP:AE=DF: DA=1:3,则FP:BE=1:6=FG:BG,即BG=6GF;
④因为点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,当点E,F分别是AB,AD中点时,CG⊥BD;
⑤∠BGE=∠BDG ∠DBF=∠BDG ∠GDF=60°.
解答: ①∵ABCD为菱形,∴AB=AD,
∵AB=BD,∴△ABD为等边三角形,
∴∠A=∠BDF=60°,
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本选项正确;
②∵∠BGE=∠BDG ∠DBF=∠BDG ∠GDF=60°=∠BCD,
即∠BGD ∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°,
∴∠BGC=∠DGC=60°,
过点C作CM⊥GB于M,CN⊥GD于N(如图1),
则△CBM≌△CDN(AAS),
∴S四边形BCDG=S四边形CMGN,
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=CG,CM=CG,
∴S四边形CMGN=2S△CMG=2××CG×CG=CG2,故本选项错误;
③过点F作FP∥AE于P点(如图2),
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=FP:=1:6,
∵FP∥AE,
∴PF∥BE,
∴FG:BG=FP:BE=1:6,
即BG=6GF,故本选项正确;
④当点E,F分别是AB,AD中点时(如图3),
由(1)知,△ABD,△BDC为等边三角形,
∵点E,F分别是AB,AD中点,
∴∠BDE=∠DBG=30°,
∴DG=BG,
在△GDC与△BGC中,
∴△GDC≌△BGC,
∴∠DCG=∠BCG,
∴CH⊥BD,即CG⊥BD,故本选项错误;
⑤∵∠BGE=∠BDG ∠DBF=∠BDG ∠GDF=60°,为定值,
故本选项正确;
综上所述,正确的结论有①③⑤,共3个,
故选B.
此题综合考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,作出辅助线构造出全等三角形,把不规则图形的面转化为两个全等三角形的面积是解题的关键.
在本单元的其他题目,也不可小瞧哦,现在让我们开始去探索中考真题吧。