二次函数作为中考数学压轴题,屡考不限,考查的方式多种多样,每年层出不穷,花样多,难度大,属中考拉分题,是区分学霸还是学渣的一道题,为学生选拔提供依据。
有人统计二次函数有三十多个模型可考,包括面积最值、平行四边形存在性,矩形存在性、菱形存在性、正方形存在性、相似三角形存在性、等腰三角形存在性、直角三角形存在性、线段最值、相等角存在性、二倍角存在性、对称点存在性、45度角存在性、抛物线平移、抛物线翻折、图形旋转等等。
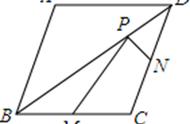
今天笔者拿来一道菱形问题存在性压轴题,通过解题思路分析和步骤示范,旨在帮助同学们解决这类特殊四边形存在性问题的一般性解题方法。通常可通过菱形的性质来寻求动点的坐标,包括平行四边形的特性、四条边相等的特性、对角线相互垂直的特性,可进行分类讨论,“盲目”地求得满足条件的动点。这种盲目法适合一切以上提到的特殊四边形的存在性问题。
小题不丢分,大题多得分,关注 提高解题能力