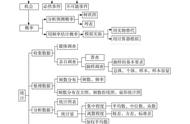
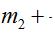第一章 证明(二)
一、公理
1、三边对应相等的两个三角形全等(可简写成“边边边”或“SSS”)。
2、两边及其夹角对应相等的两个三角形全等(可简写成“边角边”或“SAS”)。
3、两角及其夹边对应相等的两个三角形全等(可简写成“角边角”或“ASA”)。
4、全等三角形的对应边相等、对应角相等。
推论:两角及其中一角的对边对应相等的两个三角形全等(可简写成“角角边”或“AAS”)。
二、等腰三角形
1、等腰三角形的性质
( 1 )等腰三角形的两个底角相等(简称:等边对等角)。
(2)等腰三角形顶角的平分线、底边上的中线、底边上的高互相 重合(三线合一)。
2、等腰三角形的其他性质
(1)等腰直角三角形的两个底角相等且等于45°
( 2 )等腰三角形的底角只能为锐角,不能为钝角(或直角),但 顶角可为钝角(或直角)。
(3)等腰三角形的三边关系:设腰长为a,底边长为b,则

等腰三角形的三角关系:设顶角为顶角为∠A,底角为∠B、∠C, ∠A=180°-2∠B,∠B=∠C=

。
3、等腰三角形的判定
( 1 )如果一个三角形有两个角相等,那么这两个角所对的边也相 等(简称:等角对等边)。
(2)有两条边相等的三角形是等腰三角形。
三、等边三角形
1、性质:
(1)等边三角形的三个角都相等,并且每个角都等于60°。
(2)三线合一。
2、判定:
(1)三条边都相等的三角形是等边三角形。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是60°的等腰三角形是等边三角形。
四、直角三角形
1、直角三角形的性质
(1)直角三角形的两个锐角互余
(2)在直角三角形中,30°角所对的直角边等于斜边的一半。
(3)直角三角形斜边上的中线等于斜边的一半
(4)勾股定理:直角三角形两直角边a,b的平方和等于 斜边c的平方,即 a 2 b 2 =c 2 。
2、其它性质
(1)直角三角形斜边上的高线将直角三角形分成的两个三角形和原三角形相似。
(2)常用关系式:由三角形面积公式可得:两直角边的积=斜边与斜边上的高的积。
3、直角三角形的判定
(1)有一个角是直角的三角形是直角三角形。
(2)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
(3)勾股定理的逆定理
如果三角形的三边长a,b,c有关系a2 b2=c2,那么这个三角形是直角三角形。
4、直角三角形全等的判定
对于特殊的直角三角形,判定它们全等时,还有HL定理(斜边、直角边定理):有斜边和一条直角边对应相等的两个直角三角形全等(可简写成“斜边、直角边”或“HL”)。
五、角的平分线及其性质与判定
1、角的平分线:
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
2、角的平分线的性质定理:
角平分线上的点到这个角的两边的距离相等。
定理:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等。
3、角的平分线的判定定理:
在一个角的内部,且到角的两边距离相等的点在这个角的平分线上。
六、线段垂直平分线的性质与判定
1、线段的垂直平分线:
垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线。
3、线段垂直平分线的性质定理:
线段垂直平分线上的点和这条线段两个端点的距离相等。
定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等。
4、线段垂直平分线的判定定理:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
七、反证法
八、互逆命题、互逆定理
1、在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题。
2、如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理。
第二章 一元二次方程
一、一元二次方程
1、一元二次方程定义
含有一个未知数,并且未知数的最高次数是2的整式方程叫做一 元二次方程。
2、一元二次方程的一般形式

它的特征是:等式左边是一个关于未知数x的 二次多项式,等式右边是零,其中 ax 2 叫做二次项,a叫做二次项系数;bx叫 做一次项,b叫做一次项系数;c叫做常数项。
二、一元二次方程的解法
1、直接开平方法
直接开平方法适用于解形如(x a)2=b的一元二次方程。当