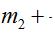五、等腰梯形
1、等腰梯形的定义
两腰相等的梯形叫做等腰梯形。
2、等腰梯形的性质
(1)等腰梯形的两腰相等,两底平行。
(2)等腰梯形同一底上的两个角相等,同一腰上的两个角互补。
(3)等腰梯形的对角线相等。
(4)等腰梯形是轴对称图形,它只有一条对称轴,即两底的垂直 平分线。
3、等腰梯形的判定
(1)定义:两腰相等的梯形是等腰梯形
(2)定理:在同一底上的两个角相等的梯形是等腰梯形
(3)对角线相等的梯形是等腰梯形。(选择题和填空题可直接 用)
六、三角形中的中位线
1、三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线。
2、三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
3、常用结论:任一个三角形都有三条中位线,由此有:
结论1:三条中位线组成一个三角形,其周长为原三角形周长的一半。
结论2:三条中位线将原三角形分割成四个全等的三角形。
结论3:三条中位线将原三角形划分出三个面积相等的平行四边形。
结论4:三角形一条中线和与它相交的中位线互相平分。
结论5:三角形中任意两条中位线的夹角与这夹角所对的三角形的顶角相等。
七、有关四边形四边中点问题的知识点
1、顺次连接任意四边形的四边中点所得的四边形是平行四边形;
2、顺次连接矩形的四边中点所得的四边形是菱形;
3、顺次连接菱形的四边中点所得的四边形是矩形;
4、顺次连接等腰梯形的四边中点所得的四边形是菱形;
5、顺次连接对角线相等的四边形四边中点所得的四边形是菱形;
6、顺次连接对角线互相垂直的四边形四边中点所得的四边形是矩形;
7、顺次连接对角线互相垂直且相等的四边形四边中点所得的四边形是正方形;
第四章 视图与投影
一、投影
1、投影:物体在光线的照射下,在地面上或墙壁上留下它的影子,这就是投影现象。
2、平行投影:太阳光线可以看成平行光线,像这样的光线所形成的投影称为平行投影。
3、中心投影:探照灯、手电筒、路灯和台灯的光线可以看成是从一点发出的,像这样的光线所形成的投影称为中心投影。
二、视点、视线、盲区
第五章 反比例函数
一、反比例函数的概念
一般地如果两个变量x,y之间的关系可以表示

的形式,那么称y是x的反比例函数。(反比例函数的解析式也可以写成

的形式。自变量x的取值范围是x

0的一切实数,函数的取值范围也是一切非零实数。)
二、反比例函数的图象
反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限,它们关于原点对称。由于反比例函数中自变量x