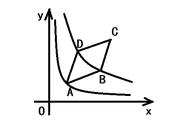
【分析】这类题的特征一般是通过条件求图象上某一点的坐标,然后根据xy=K,从而确定解析式.第一问,根据AC=BC=5/2,过C点作CE⊥AB于E,则E为AB的中点,则AE=BE=2,由于AB⊥x轴,所以C点纵坐标为2,在Rt△BEC中,求出CE的长为3/2,因为OA=4,所以C点横坐标为4一3/2=5/2,则C点坐标确定,所以反比例函数解析式可得.第二问,由于BD=BC=5/2,所以AD=AB一BD=4一5/2=3/2,所以D点纵坐标为3/2,而C点纵坐标还是2,C到AB的距离长CE=3/2,若设出A点坐标为(m,0),则C点坐标为(m一3/2,2),D点坐标为(m,3/2),由于C,D两点都在反比例函数图像上,利用xy=K建立方程可求得m,进而求得C点坐标,利用勾股定理可得OC的长.
解:(1)过C点作CE⊥AB于E,如图,

∵AC=BC,AB=4,∴AE=BE=2,在Rt△BCE中,BC=5/2,BE=2,∴CE=3/2,∵OA=4,∴C点坐标为(5/2,2),又C点在y=K/x的图象上,∴xy=K,即K=2×5/2=5,所以反比例函数的图象为y=5/x.(x>0).
(2).如图,作CF⊥x轴,垂足为F,

设A点的坐标为(m,0),∵BD=BC=5/2,AB=4,∴AD=3/2,∴D点坐标为(m,3/2),由(1)知CE=3/2,AE=BE=2,∴C点坐标为(m一3/2,2),∵C,D两点都在y=K/x的图象上,∴3m/2=2(m一3/2),解得m=6,∴C点坐标为(9/2,2),∴OF=9/2,CF=2,在Rt△OFC中,由勾股定理可得,OC=√97/2.
6.如图,矩形AOCB的两边OC,OA分别在x轴,y轴上,点B的坐标为(一20/3,5),D是AB上的一点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图象上,求该反比例函数的解析式.

【分析】求反比例函数解析式,实质上是求系数K,那么就只需要一个条件,大多数是求图象上点的坐标,本题只要求出E点坐标即可,由于折叠A点落在E处,则OA=BC=OE=5,过E作EF⊥x轴于F,则△OEF∽△OBC,则OE/OB=EF/BC=OF/OC,由题意知BC=5,OC=20/3,则OB=25/3,可求出OF,EF,则E点坐标求出,反比例函数解析式可求出.当然也可用三角函数求E点坐标.
解:如图,过E点作EF⊥x轴于F,设过E点的反比例函数解析式为y=K/x,(K≠0).