由矩形AOCB知BC⊥x轴,∴△OEF∽△OBC,∴OE/OB=EF/BC=OF/OC,∵B点坐标为(一20/3,5),∴BC=5,OC=20/3,由于△ADO沿OD翻折,A点落在OB上E处,∴OE=OA=BC=5,在Rt△BCO中,由勾股定理求得OB=25/3,∴可求得,EF=3,OF=4,∴E点坐标为(一4,3),代入y=K/x,得K=一12,所以反比例函数解析式为y=一12/x.
方法四,利用待定系数法求解析式
7.已知y1与x成正比例,y2与x成反比例,若y=y1 y2的图象经过点(1,2),(2,1/2),求y与x的函数解析式.
【分析】这种题型,根据题意,设出对应的函数解析式,利用条件列方程组,解出相应的待定系数即可,注意待定系数在不同的函数中应用不同的字母.
解:∵y1与x成正比例,∴设y1=Kx(K≠0),∵y2与x成反比例,∴设y2=m/x(m≠0),由y=y1 y2得,y=Kx十m/x,又∵y=Kx m/x的图象经过(1,2)和(2,1/2)两点,∴可得

8.已知y=y1 y2,y1与x成正比例,y2与x²成反比例,且x=2与x=3时,y的值都等于19,求y与x间的函数关系式
解∵y1与x成正比例,∴设y1=Kx(K≠0),∵y2与x²成反比例,∴设y2=m/x²(m≠0),∴y=y1 y2=Kx十m/x,∵当x=2时y=19,当x=3时y=19,∴可得

方法五.利用图形的面积求解析式
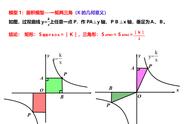
9.如图,点A在双曲线y=1/x上,点B在双曲线y=K/x上,且AB∥x轴,C,D两点在x轴上,若矩形ABCD的面积为6,求点B所在双曲线对应的函数解析式.

【分析】反比例函数y=K/x的系数K具有一定的几何意义,|K|等于图象上任意一点向两坐标轴所作垂线与坐标轴所围成的矩形的面积.如图