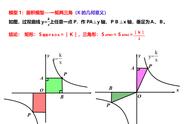
|K|=S矩形AEOC=S矩形BFOD,|K|/2=2S△AOC=2S△BOD=2S△AOE=S△BOF.灵活运用K的几何意义,通过面积求出K,也就求得解析式.所以延长BA交y轴于点E,则四边形AEOD,BEOC均为矩形,则由题意得,S矩形AEOD=1,S矩形BEOC=|K|,∴|K|=1 6=7,由于反比例函数图象在第一,三象限,K>0,∴K=7,∴反比例函数解析式为y=7/x.如图.

解:延长BA交y轴于点E,由题意可知S矩形AEOD=1,S矩形BEOC=K,∵S矩形ABCD=6,∴K一1=6,K=7,∴B点所在双曲线对应的函数解析式是y=7/x.
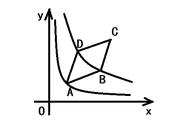
10.如图,A,B是双曲线y=K/x(K≠0)上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,若△ADO的面积为1,D为OB的中点,求反比例函数的解析式.

【分析】反比例函数有些与面积有关的习题,灵活运用|K|的几何意义,结合题中的条件建立关于K的方程,是这类题的常见的解法,本题过B作BE⊥x轴于E,由于D为OB的中点,则BE=2CD,AD=AC一CD=AC一BE/2,OE=2OC,如图,

设A点坐标为(x,K/x),(K>0),∵C,A两点横坐标都为x,则B点横坐标2x,∴B点坐标为(2x,K/2x),∴CD=k/4x,AD=K/x一K/4x,∵S△AOD=1,即1/2(K/x一K/4x)x=1,解得K=8/3.所以反比例函数解析式为y=8/3x.(反比例函数有这样的优势,通过设坐标,引进系数K,也就引进了面积,这一点同学们多体会一下).
方法六.利用实际问题的关系求解析式
11.某运输队要运300t物资到江边防洪.
(1)运输时间t(单位:h)与运输速度v(单位:t/h)之间有怎样的函数关系?
(2)运了一半时,接到防洪指挥部命令,剩下的物资要在2h之内运到江边,则运输速度至少为多少?
【分析】实际问题往往通过具体的量的关系,抽象为数学模型,用对应模型的数学知识解决实际问题.(1)本题数量关系为:物资总量=运输时间×运输速度,由于物资总量300t一定,所以运输时间与运输速度成反比例关系即t=300/v.(2)运输物资剩下一半即150t时,剩下的要在2h运到江边,所以运输速度至少为150÷2=75(t/h).(实际问题中的数量关系求反比例函数解析式,必须是a×b=c,c一定的数学模型).
12.某汽车的功率P(单位:W)为一定值,它的速度v(单位:m/s)与它所受的牵引力F(单位:N)有关系:v=P/F,且当F=3000时,v=20.
(1)这辆汽车的功率是多少瓦?请写出这一函数的解析式.
(2)当它所受的牵引力为2500N时,汽车的速度为多少?
(3)若限定汽车的速度不超过30m/s,则牵引力在什么范围?
解:(1)由v=P/F,得P=Fv=3000×20=60000所以这辆汽车的功率为60000W,此函数解析式为v=60000/F.
(2)当F=2500N时,代入v=60000/F,得v=60000÷2500=24,所以汽车的速度为24m/s.
(3)由v≤30m/s,∴60000÷F≤30,∵F>0,∴F≥2000,所以牵引力大于或等于2000N.
【总结】求反比例函数解析式,一般不太难,同学们把常见的方法掌握好,求出解析式为进一步攻克难题打下基础关.
感谢大家的关注、转发、点赞、交流!
,