一.概念描述
现代数学:旋转变换简称旋转。欧式几何中的一种重要变换。在欧氏平面上(欧氏空间重),让每一点P绕一固定点(同定轴线)旋转一个定角,变成另一点P’,如此产生的变换称为平面上(空间中)的旋转变换。此固定点(固定直线)称为旋转中心(旋转轴),该定角称为旋转角。
初中数学对于旋转没有给出严格的定义,只是借助图形直观表述。如2009年人教版教材九年级上册第56页先出示下图,然后说:像这样,把一个平面图形绕着平面内某一点O转动一个角度,就叫作图形的旋转,点O叫作旋转中心,转动的角叫作旋转角。

小学数学:小学阶段是结合具体实例直观认识旋转现象,通过在方格纸上作已知图形经旋转变换后的图形来获取运动体验。小学教材没有对旋转给出明确的定义。
二.概念解读
旋转是图形运动的一种形式,是图形变换的一种。它与平移同属于图形变换中的全等变换。从“旋转”这个词的发音来看,我们可以从字面意思把旋转理解为“围绕着中心转”。
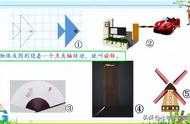
①旋转是现实生活中广泛存在的现象,生活中有很多物体在做着旋转运动。比如风扇、车轮、旋转门、秋千、跷跷板等,但生活中的旋转现象并不是绝对意义上的数学中的旋转。要研究数学中的旋转变换,教师要引导学生借助相关的生活经验,关注旋转前后图形的大小和形状有没有发生改变、对应点到旋转中心的距离是否相等、对应点与旋转中心所连线段的夹角是否等于旋转角等,要抓住旋转的三要素(旋转中心、方向和角度)来辨别旋转运动。
假如我们把下图钟面上的指针看作平面图形,那么表盘的中心就是旋转中心,两根表针转动时形成的角就是旋转角。

在这里,教师要认识到摆动也是日常生活中常见的旋转现象。
比如: