01
一、数位顺序表
知识点:
1.每相邻的两个计数单位之间的进率是10 。
2.亿级、万级、个级分别有四个数位和四个计数单位。
3.万级包括的数位有( ),亿级包括的计数单位有( ),个级包括的数位和计数单位分别是( )和( )。
4.8800888000这个数是( )位数,最高位上的8表示( ),右边起第六位上的8表示( )。
我来判断(对的打“√”,错的打“×” )。
1.在十进制计数法中,每相邻两个计数单位间的进率都是10。 ( )
2.个、十位、百、千、万等都是计数单位。 ( )
3. 99999999这个数左数第七位的8表示“8个千万”。( )
二、我能“读”也能“写”。
1.读数的方法:1. 四位分级;2.从最高位起一级一级的读,每一级都按个级的读法读,亿级读完再在后面加“亿”字,万级读完在后面加“万”字;3.每一级末尾不管有几个零都不读,其它数位上有一个零或连续几个零,都只读一个零。
练一练:
550505000读作:
960060007读作:
30220890 读作:
90600700 读作:
2.写数的方法:从最高位起,一级一级的写,哪一位数位上没有数字,就用0代替。
练一练:
四千三百万零三万 写作:
七千万零九十一 写作:
七千三百零五万零五百零五 写作:
一亿零四百零一万零六百 写作:
3.800800800要读一个零,你觉得对吗?试着读读看
三、大数我能改写和比较。
1.亿以内数比较大小的方法。
位数不同时,位数的数大于位数少的数。
位数相同时,从最高位比起,最高位上的数大这个数就大;如果最高位上的数字相同,就比较下一位,直到比较出大小为止。
2.改写以“万”或“亿”为单位的数的方法。
以“万”为单位,就要把末尾的四个0去掉,再添上万字;以“亿”为单位,就要把末尾八个0去掉,再添上亿字。
练一练:
1.改写下面各数。
32100000=( )万
169000000=( )万
18600000000 =( )亿
390000000000=( )亿
2.比较下列各数大小。
1000000 ○ 999999 9120000○ 9120001
876543 ○ 876534 260000 ○ 26万
342300○ 343200 3024999 ○ 302万
1、 近似数。
“四舍五入”:法四舍五入(或者保留)到哪一位,就看它的下一位,如果下一位上是0到4,就将后面的舍去(舍去即将后面的改为0)。如果下一位上是5到9,就向前进一,再把后面的舍去。
练习题
1.精确到百位,看( )位,
精确到千位,看( )位,
精确到万位,看( )位,
精确到亿位,看( )位。
2.用四舍五入法求下列近似数。
5782562≈( )万
157865296≈( )万
458587436≈( )亿
综合练习。
1. 10个一万是( ),10个十万是( ),10个百万是( ),10个千万是( )。
2.万级包括哪四个数位( )( )( )( )。十万位相应的计数单位是( )。
3.从个位起,第( )位是万位,第八位是( )。
4. 500505000是一个( )位数,最高位上的“5”表示( )个( ),中间的“5”表示( )个( ),最后的“5”表示( )个( )。
5.20800600 读作:( )
50056000 读作:( )
三千零二十八万六千六百 写作:( )
五十三万零三十 写作:( )
6.我国的领土面积大约是九百六十万平方千米。
写作:( ),它是( )位数,最高位是( )位,是由( )个百万和( )个十万组成的。
7.改写下面各数。
4860000=( )万
15800000=( )万
1200000000 =( )亿
843000000000=( )亿
8.将下列各数从大到小排列。
36000 36万 30600 300600 三十万零六
02
二单元《线与角》
线的认识
1、 认识直线、线段与射线,会用字母正确读出直线、线段和射线。
直线:可以向两端无限延伸;没有端点。
读作 :直线AB或直线BA。
线段:不能向两端无限延伸;有两个端点。
读作:线段AB或线段BA。
射线:可以向一端无限延伸;有一个端点。
读作:射线AB(只有一种读法,从端点读起。)
补充知识点:
1、画直线。
过一点可画无数条直线;过两点只能画一条直线;明确两点之间的距离,线段比曲线、折线要短(两点之间线段最短)。
2、直线、射线可以无限延长。因为直线没有端点,射线只有一个端点,所以不可以测量,没有具体的长度。如:直线长4厘米。是错误的。只有线段才能有具体的长度。
平移与平行
1、在同一平面内,永不相交的两条直线叫做平行线。
2、能够借助实物,平面图形或立体图形,寻找出图中的平行线。
相交与垂直:
1、相交与垂直的概念。当两条直线相交成直角时,这两条直线互相垂直。这两条直线的交点叫做垂足。(两条直线互相垂直说明了这两条直线的位置关系:必须相交,相交还要成直角。)
2、 点到直线之间垂线段最短。
旋转与角
1、角的概念。由一点引出两条射线所组成的图形叫做角。角是由一个顶点和两条边组成的。
2、认识平角、周角。
平角 :角的两边在同一直线上,(像一条直线),平角等于180°,等于两个直角。
周角:角的两边重合,(像一条射线),周角等于360°,等于两个平角,四个直角。
3、角的分类:小于90度的角叫做锐角;等于90度的角叫做直角;大于90度小于180度的角叫做钝角;等于180度的角叫做平角;等于360度的角叫做周角。
角的度量
1、认识度。将圆平均分成360份,把其中的1份所对的角叫做1度,记作1°,通常用1°作为度量角的单位。
2、认识量角器。量角器是把半圆平均分成180份,一份表示1度。量角器上有中心点、0刻度线、内刻度线、外刻度线。
3、量角器的使用方法。“两合一看”,“两合”是指中心点与角的顶点重合;0刻度线与角的一边重合。“一看”就是要看角的另一边所对的量角器的刻度。
4、 看角的度数时要注意是看外刻度还是内刻度。角的开口向左看外刻度线,角的开口向右看内刻度线。
画角
1、用量角器画指定度数的角的方法。
画一条射线,中心点对准射线的端点,0刻度线对准射线(两合),对准量角器相应的刻度点一个点(一看),把点和射线端点连接,然后标出角的度数。
2、30度、60度、90度、45度、75度、105度、135度、120度和150度用三角板比较方便。
练习题
一、请在括号里对的画“√”,错的画“×”。
1、线段是直线上两点之间的部分。( )
2、过一点只能画出一条直线。( )
3、一条射线长6厘米。( )
4、手电筒射出的光线可以被看成是线段。( )
5、过两点只能画一条直线。( )
6、角的两边越长,角的度数越大。( )
二、填空。
1、直线有( )个端点,它可以向两端无限延长。
2、直线上两点之间的一段叫( ),它有( )个端点。
3、射线有( )个端点,它可以向一端无限延长。
4、当两条直线相交成直角时,这两条直线( ),这两条直线的交点叫做( )。
5、锐角的度数小于( )度;大于( )度而小于180度的角叫做钝角;( )度的角是直角,( )度的角是平角,( )度的角是周角。
6、1个周角=( )度=( )个平角=( )个直角。

03
第三单元 乘法
1、 列竖式计算。
178×46=
408×25=
37×235=
380×23=
2、探索规律。
①123456789×9×2=2222222202,
123456789×9×3=3333333303,
观察上面两个算式,写出下面两式的结果:
123456789×9×4=( ),
123456789×45=( )。
②33333×66667=2222211111,
333333×666667=222222111111,
观察上面两个算式,写出下面两式的结果
3333333×6666667=( ),
33333333×66666667=( )。
一、想一想,填一填。
1、最小的两位数与最大的三位数的积是( )。
2、200个18是( ),125的40倍是( )。
3、 特快列车1小时约行160千米,6小时可行( )千米。
4、在○填上“>”、“<”或“=”。
180×5○160×6 47×100○470×10
5、光明小学有789人,大约是( )人。
6、根据6×50=300直接写出下面两题的积。
18×50=( ) 42×50=( )
7、一架飞机的速度可达每小时900千米,可以写作( )。
二、用心选一选。
1、一个因数不变,另一个因数扩大10倍,积( )。
A、不变 B、扩大10倍 C、缩小10倍
2、125×80的积的末尾有( )个零。
A、2 B、3 C、4
3、三位数乘两位数积是( )。
A、四位数 B、五位数 C、四位数或五位数
4、美园小区有五栋楼房,每栋有120户人家,小区共有( )户人家。
A、600 B、500 C、125
三、、计算题要仔细。
1、估算。
603×21≈ 399×42≈ 538×48≈
四、解决问题。
1、星月饭店平均每天要用掉258双一次性筷子。这个饭店每个月大约要用掉多少双一次性筷子?(按30天计算)

第一单元 小数除法
1、除数是整数的小数除法计算法则:除数是整数的小数除法,按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添0再继续除。
2、除数是小数的小数除法计算法则:除数是小数的除法,先移动除数的小数点,使它变成整数;除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的,在被除数末尾用0补足),然后按照除数是整数的小数除法进行计算。
3、连除的算式可以写成被除数除以几个数的积,但除以几个数的积时,必须给这个相乘的式子加上小括号。
4、 在小数除法中的发现:
①当除数不为0时,除数大于1时,商小于被除数。如:3.5÷5=0.7
②当除数不为0时,除数小于1时,商大于被除数。如:3.5÷0.5=7
�当除数不为0时,除数等于1时,商等于被除数。如:3.5÷1=3.5
5、小数除法的验算方法:
①商×除数=被除数(通用) ②被除数÷商=除数
6、商的近似数:根据要求要保留的小数位数,决定商要除出几位小数,再根据“四舍五入”法保留一定的小数位数,求出商的近似数。例如:要求保留一位小数的,商除到第二位小数可停下来;要求保留两位小数的,商除到第三位小数停下来……如此类推。
7、循环小数:
A、小数部分的位数是有限的小数,叫做有限小数。如,0.37、1.4135等。
B、小数部分的位数是无限的小数,叫做无限小数。如5.3… 7.145145…等。
C、一个数的小数部分,从某位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。(如5.3… 3.12323… 5.7171…)
D、一个循环小数的小数部分,依次不断重复的数字,叫做小数的循环节。(如5.333… 的循环节是3, 4.6767…的循环节是67, 6.9258258…的循环节是258)
E、用简便方法写循环小数的方法:
①只写一个循环节,并在这个循环节的首位和末位上面记一个小圆点
②例如:只有一个数字循环节的,就在这个数字上面记一个小圆点,5.333…写作5.3 ;有两位小数循环的,就在这两位数字上面,记上小圆点,7.4343…写作7.4 3 ;有三位或以上小数循环的,在首位和末位记上小数点,10.732732…写作10.732
8、除法中的变化规律: ①商不变性质:被除数和除数同时扩大或缩小相同的倍数( 0除外),商不变。②除数不变,被除数扩大,商随着扩大。 ③被除数不变,除数缩小,商扩大。
9、小数的四则混合运算顺序与整数四则混合运算的运算顺序相同。
第二单元 轴对称和平移
轴对称:
1.轴对称图形:如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形,那条直线就叫做对称轴。两图形重合时互相重合的点叫做对应点,也叫对称点。
2.轴对称图形的性质:对应点到对称轴的距离相等,对应点连线垂直于对称轴。
3.轴对称图形具有对称性。
4轴对称图形的法:
(1)找出所给图形的关键点,如图形的顶点、相交点、端点等;
(2)数出或量出图形关键点到对称轴的距离;
(3)在对称轴的另一侧找出关键点的对称点;
(4)按照所给图形的顺序连接各点,就画出所给图形的轴对称图形。
平移:
1.平移的定义:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
2.平移的基本性质:
(1)平移不改变图形的形状和大小,只改变图形的位置。
(2)经过平移,对应线段,对应角分别相等;对应点所连的线段平行且相等。
3.平移图形的画法:
(1)确定平移的方向与距离。
(2)将关键点按所需方向平移所需距离。
(3)按原来图形的连接方式依次连接各对应点。
4、平移几格并不是指原图形和平移后的新图形之间的空格数,而是指原图形的关键点平移的格数。
设计图案的基本方法:平移、对称
1.运用平移设计图案的方法:
(1)选好基本图案;(2)根据所选的基本图案确定平移的格数和方向;
(3)平移,描出对应点; (4)按顺序连接对应点
2.运用对称设计图案的方法:
(1)先选好基本图案;
(2)依据基本图案的特点定好对称轴;
(3)选好关键点,并描出关键点的对应点;
(4)按顺序连接对应点,画出基本图形的对称图形
第三单元 倍数和因数
像0,1,2,3,4,5,6,…这样的数是自然数。
像-3,-2,-1,0,1,2,3,…这样的数是整数。
我们只在自然数(零除外)范围内研究倍数和因数。
倍数与因数是相互依存的关系,要说清谁是谁的倍数,谁是谁的因数。
补充知识点:一个数的倍数的个数是无限的,因数个数是有限的。
一个数最小的因数是1,最大的因数是它本身;一个数最小的倍数是它本身,没有最大的倍数。
(一)2,5的倍数的特征
2的倍数的特征: 个位上是0,2,4,6,8的数是2的倍数。
5的倍数的特征: 个位上是0或5的数是5的倍数。
偶数和奇数的定义: 是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
补充知识点:
既是2的倍数,又是5的倍数的特征:个位上是0的数既是2的倍数,又是5的倍数。(既是2的倍数,又是5的倍数都是整十数,最小的两位数是10,最小的三位数是100)
(二)3的倍数的特征
一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
同时是2和3的倍数的特征: 个位上的数是0,2,4,6,8,并且各个数位上的数字的和是3的倍数的数,既是2的倍数,又是3的倍数。(同时是2和3的倍数,一定是6的倍数,最小的是6。)
同时是3和5的倍数的特征: 个位上的数是0或5,并且各个数位上的数字的和是3的倍数的数,既是3的倍数,又是5的倍数。(同时是3和5的倍数,一定是15的倍数,最小的是15。)
同时是2,3和5的倍数的特征: 个位上的数是0,并且各个数位上的数字的和是3的倍数的数,既是2和5的倍数,又是3的倍数。(同时是2,3和5的倍数,一定是30的倍数,最小的两位数是30,最小的三位数是120)
9的倍数的特征:一个数各个数位上的数字的和是9的倍数,这个数就是9的倍数,它也一定是3的倍数。
㈣找因数
在1~100的自然数中,找出某个自然数的所有因数。方法:1、运用乘法算式,思考:哪两个数相乘等于这个自然数,那么这两个乘数就是这个数的因数。
2、运用除法算式,思考这个数除以几能整除,那么除数和商就是这个数的因数。
补充知识点:
一个数的因数的个数是有限的。其中最小的因数是1,最大的因数是它本身。找一个数的因数,通常用列举的方法,可一对一对的写出来,也可按从小到大的顺序来写。
㈤找质数
一个数只有1和它本身两个因数,这个数叫作质数。
一个数除了1和它本身以外还有别的因数,这个数叫作合数。
1既不是质数也不是合数。
判断一个数是质数还是合数的方法:
一般来说,首先可以用“2,5,3的倍数的特征”判断这个数是否有因数2,5,3;如果还无法判断,则可以用7,11等比较小的质数去试除,看有没有因数7,11等。只要找到一个1和它本身以外的因数,就能肯定这个数是合数。如果除了1和它本身找不到其他因数,这个数就是质数。
㈥数的奇偶性
运用“列表”“画示意图”等方法发现规律:
小船最初在南岸,从南岸驶向北岸,再从北岸驶回南岸,不断往返。通过“列表”“画示意图”的方法会发现“奇数次在北岸,偶数次在南岸”的规律。
通过计算发现奇数、偶数相加奇偶性变化的规律:
偶数 偶数=偶数 奇数 奇数=偶数 偶数 奇数=奇数
偶数-偶数=偶数 奇数-奇数=偶数 偶数-奇数=奇数
奇数-偶数=奇数
偶数×偶数=偶数 偶数×奇数=偶数 奇数×奇数=奇数
第四单元 多边形面积
㈠比较图形的面积
借助方格纸,能直接判断图形面积的大小。
平面图形面积大小的比较有多种方法:
根据图形面积的大小,可以直接进行比较;可以借助参照物进行比较;可以运用重叠的方法进行比较;借助方格,利用数方格的的方法进行比较;直接计算面积后再进行比较等。
图形面积相同,其形状可以是不同的。
补充知识点:
确定一个图形面积的大小,不仅是根据图形的形状,更重要的是根据图形所占格子的多少来确定。
㈡地毯上的图形面积
知识点:
根据地毯上所给图案探求不规则图案面积的计算方法。
直接通过数方格的方法,得出答案的面积。
将图案进行“化整为零”式的计算,即根据图案的特点,将整体的图案分割为若干个相同面积的小图案,通过求小图案的面积,得出整个图案的面积。
采用“大面积减小面积”的方法,即通过计算相关图形的面积,得到所求的面积。
补充知识点:
在解决问题时,策略和方法是多种多样的。
㈢动手做
认识平行四边形、三角形与梯形的底和高。
从平行四边形一边的某一点到对边画垂直线段,这条垂直线段就是平行四边形的高,这条对边是平行四边形的底。
三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
从梯形的两条平行线中的一条上的某一点到对边画垂直线段,这条垂直线段就是梯形的高,这条对边就是梯形的底。
高和底的关系是对应的。
用三角板画出平行四边形的高的方法:
把三角板的一条直角边与平行四边形的一条边重合,让三角板的另一条直角边过对边的某一点。从这一点沿着三角板的另一条直角边向它的对边画垂线,这条垂线(从点到垂足)就是平行四边形一条边上的高。
注意:从一条边上的任意一点可以向它的对边画高,也可以从另一条边上的任意一点向它的对边画高。
用三角板画出三角形的高的方法:
把三角板的一条直角边对准三角形的一个顶点,另一条直角边与这个顶点的对边重合。从这个顶点沿着三角板的另一条直角边向它的对边画垂线,这条垂线(从顶点到垂足)就是三角形形一条边上的高。
用三角板画梯形的高的方法:
用同样的方法,画出梯形两条平行线之间的垂直线段,就是梯形的高。
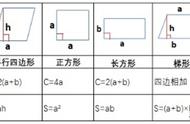
(一)平行四边形的面积
平行四边形的面积=拼成的长方形的面积
长方形的长就是平行四边形的底;长方形的宽就是平行四边形的高。
因此:平行四边形面积=底×高
如果用S表示平行四边形的面积,用a和h分别表示平行四边形的底和高,那么,平行四边形的面积公式可以写成:S=a h
补充知识点:
当平行四边形的底和高相同时,其面积也是相同的。
(二)三角形的面积
三角形面积=两个相同三角形拼成的平行四边形的面积÷2
三角形的底和高,也就是平行四边形的底和高。
因此:三角形面积=平行四边形的面积÷2=底×高÷2
如果用S表示三角形的面积,用a和h分别表示三角形的底和高,那么,三角形的面积公式可以写成:S=a h÷2
补充知识点:
决定三角形面积的大小的因素不是图形的形状,而是三角形的底与高的长度,只要底和高相同,不同形状的三角形的面积也是相同的。
(三)梯形的面积
梯形面积=两个相同梯形拼成的平行四边形的面积÷2
梯形的上底与下底的和就是平行四边形的底,梯形的高就是平行四边形的高。
因此:梯形面积=平行四边形面积÷2=底×高÷2=(上底 下底)×高÷2
如果用S表示梯形的面积,用a和b分别表示梯形的上底和下底,用h表示梯形的高,那么,梯形的面积公式可以写成:S= (a b)h÷2
补充知识点:
决定梯形面积的大小的因素不是图形的形状,而是梯形的上、下底之和与高的长度,只要上下底的和与高相同,不同形状的梯形的面积也是相同的。
等底等高的三角形的面积相等。
等底等高的平行四边形的面积相等。
第五单元 分数的意义
㈠分数的再认识
整体“1”的含义:一个物体或一些物体都可以看作一个整体,这个整体可以用自然数“1”来表示,通常叫做整体“1”。
分数的意义:把整体“1”平均分成若干份,其中的一份或几份,可以用分数表示。分母是几,整体就被分成了几份,分子是几,就表示其中的几份。
分数对应的“整体”不同,分数所表示的部分的大小或具体数量也不一样,即分数具有相对性。同一个分数对应的整体大,表示的具体数量就大;对应的整体小,表示的具体数量就小。同一个分数表示的具体数量大,对应的整体就大;表示的具体数量小,对应的整体就小。
㈡(真分数与假分数)
理解真分数、假分数、带分数的意义。
像 、 、 、 ,…这样的分数叫作真分数。特点:分子都比分母小;分数值小于1。
像 、 、 、 ,…这样的分数叫作假分数。特点:分子比分母大,或者分子与分母相等;分数值大于或等于1。
像 ,这样的分数叫作带分数。特点:由整数和真分数两部分组成的;分数值大于1。
带分数的读法: 读作:二又四分之一。
★补充知识点:
分子是分母倍数的假分数可以化成整数; 分子不是分母倍数的假分数可以化成带分数。
㈢分数与除法
理解分数与除法的关系:被除数÷除数= (除数不为0)。
分数的分母不能是0。因为在除法中,0不能做除数,因此根据分数与除法的关系,分数中的分母相当于除法中的除数,所以分母也不能是0。可以用分数来表示两数相除的商。分数的分子相当于除法中的被除数,分母相当于除数,分数线相当于除号,分数的值相当于商。
根据分数与除法的关系把假分数化成带分数的方法:用分子除以分母,把所得的商写在带分数的整数位置上,余数写在分数部分的分子上,仍用原来的分母作分母。
把带分数化成假分数的方法:将整数与分母相乘的积加上原来的分子作分子,分母不变。
㈣分数基本性质
分数的分子和分母都乘上或除以相同的数(0除外),分数的大小不变。
分子相当于被除数,分母相当于除数,被除数和除数同时乘或除以相同的数(0除外),商不变。因此分数的分子和分母都乘或除以相同的数(0除外),分数的大小也是不变的。
求一个数是另一个数的几分之几:一个数÷另一个数= ,即比较量÷标准量= ,得到的商表示两个数的关系,没有单位名称。
㈤找最大公因数
几个数公有的因数是这几个数的公因数,其中最大的一个是它们的最大公因数。
找两个数的公因数和最大公因数的方法:
列举法:运用找因数的方法先分别找到两个数各自的因数,再找出两个数的因数中相同的因数,这些数就是两个数的公因数;再看看公因数中最大的是几,这个数就是两个数的最大公因数。
补充知识点:
其他找最大公因数的方法:
找两个数的公因数和最大公因数,可以先找出两个数中较小的数的因数,再看看这些因数中有哪些也是较大的数的因数,那么这些数就是这两个数的公因数。其中最大的就是这两个数的最大公因数。
例如:找15和50的公因数和最大公因数:
可以先找出15的因数:1,3,5,15。再判断4个数中,哪几个也是50的因数,只有1和5,1和5就是15和50的公因数。5就是它们的最大公因数。
3、如果两个数是不同的质数,那么这两个数的公因数只有1。
4、如果两个数是连续的自然数(0除外),那么这两个数的公因数只有1。
5、如果两个数具有倍数关系,那么较小的数就是这两个数的最大公因数。
㈥约分
把一个分数的分子、分母同时除以公因数,分数的值不变,这个过程叫做约分。
理解最简分数的含义:
像 这样分子、分母公因数只有1了,不能再约分了,这样的分数是最简分数。 分子与分母是相邻的自然数的分数一定是最简分数;分子分母是两个不同质数的分数一定是最简分数;分子是“1”的分数一定是最简分数。
掌握约分的方法:
约分的方法一般有两种,一种是用两个数的公因数一个一个去除,另一种是直接用两个数的最大公因数去除。
补充知识点:
比较分数大小时,分母相同的、分子相同的可以直接比较,有些时候分子分母都不相同可以采用约分后进行比较的方法。例如: ○
㈦找最小公倍数
两个数公有的倍数叫做这两个数的公倍数,其中最小的一个,叫做最小公倍数。
找两个数的公倍数和最小公倍数的方法:
1、先找出两个数各自的倍数(限制一定的范围内),再找出公有的倍数,找出两个数公有的倍数,看看这些公倍数中最小的是几,这个数就是两个数的最小公倍数。
两个数公倍数的个数是无限的,因此只有最小公倍数没有最大的公倍数。
补充知识点:
其他找公倍数和最小公倍数的方法:
2、找两个数的公倍数和最小公倍数,可以先找出两个数中较大的数的倍数(限制一定的范围内),再看看这些倍数中有哪些也是较小的数的倍数,那么这些数就是这两个数的公倍数。其中最小的就是这两个数的最小公倍数。
例如:找6和9的公倍数和最小公倍数。(50以内)可以先找出9的倍数(50以内)有:9,18,27,36,45,再从这些数中找出6的倍数18,36,18和36就是6和9的公倍数,18是最小公倍数。
3、如果两个数是不同的质数,那么这两个数的最小公倍数是两个数的乘积。
4、如果两个数是连续的自然数(0除外),那么这两个数的最小公倍数是两个数的乘积。
5、如果两个数具有倍数关系,那么较大的数就是这两个数的最小公倍数。
6、短除法求最小公倍数
㈧分数的大小
把分母不相同的分数化成和原来分数相等、并且分母相同的分数,这个过程叫作通分。
★通分的两个要点:和原来分数相等;分母相同。
■分数大小比较:
同分母分数相比较,分子越大分数越大。 同分子分数相比较,分母越小分数越大。
分子分母都不相同的分数相比较的方法:
用通分的方法把分母不相同的分数化成和原来分数相等、并且分母相同的分数,再比较大小。(把两个分数化成分子相同的分数,再比较大小)
补充知识点:通分一般以最小公倍数作分母。
第六单元 组合图形的面积
组合图形面积
知识点:了解组合图形:有几个简单的图形拼出来的图形,我们把它们叫做组合图形。
计算组合图形的面积的方法是多种多样的。一般运用的方法是“分割法”和“添补法”。
分割法,即将这个图形分割成几个基本的图形。分割图形越简洁,其解题的方法也将越简单,同时又要考虑分割的图形与所给条件的关系。
添补法,即通过补上一个简单的图形,使整个图形变成一个大的规则图形。
探索活动:成长的脚印
知识点:能正确估计不规则图形面积的大小。
能用数格子的方法,计算不规则图形的面积。
估计、计算不规则图形面积的内容主要是以方格图作为背景进行估计与计算的,所以借助方格图能帮助建立估计与计算不规则图形面积的方法。
数方格的方法:满格记为1,少于半格记为0,大于半格记为1。
尝试与猜测
鸡兔同笼 知识点:运用列表的方法(逐一列表法、跳跃列表法、折中列表法)解决类似于“鸡兔同笼”的问题,也可用“方程”来解决。
点阵中的规律 知识点:能在观察活动中,发现点阵中隐含的规律,体会到图形与数的联系。在“点阵中的规律”的活动中,通过观察前后图形中点的变化规律,推理出后续图形中点的数量。
第七单元 可能性
1、判断游戏是否公平,要看事件发生的可能性是否相等。
2、摸球游戏(用分数表示可能性的大小)
(1)通过游戏所列的条件,推测某种情况出现的概率;
(2)能判断事件发生可能性的大小,写出所有可能发生的情况,推测可能发生的结果。
知识点:用分数表示可能性的大小。
客观事件中,“不可能”出现的现象用数据表示为“可能性是0”,客观事件中,“一定能”出现的现象用数据表示为“可能性是“1”,当可能性是相等的时候,用数据表述是“ ”。
逐步体会到数据表示的简洁性与客观性。

六年级上册40个重要知识点!
1.分数乘法:
分数乘法的意义与整数乘法的意义相同,就是求几个相同加数和的简便运算。
2.分数乘法的计算法则:
分数乘整数,用分数的分子和整数相乘的积作分子,分母不变;分数乘分数,用分子相乘的积作分子,分母相乘的积作分母。但分子分母不能为零。
3.分数乘法意义
分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。一个数与分数相乘,可以看作是求这个数的几分之几是多少。
4.分数乘整数:
数形结合、转化化归
5.倒数:
乘积是1的两个数叫做互为倒数。
6.分数的倒数
找一个分数的倒数,例如3/4 把3/4这个分数的分子和分母交换位置,把原来的分子做分母,原来的分母做分子。则是4/3。3/4是4/3的倒数,也可以说4/3是3/4的倒数。
7.整数的倒数
找一个整数的倒数,例如12,把12化成分数,即12/1 ,再把12/1这个分数的分子和分母交换位置,把原来的分子做分母,原来的分母做分子。 则是1/12,12是1/12的倒数。
8.小数的倒数:
普通算法:找一个小数的倒数,例如0.25 ,把0.25化成分数,即1/4 ,再把1/4这个分数的分子和分母交换位置,把原来的分子做分母,原来的分母做分子。则是4/1。
9.用1计算法:
也可以用1去除以这个数,例如0.25 ,1/0.25等于4,所以0.25的倒数4,因为乘积是1的两个数互为倒数。分数、整数也都使用这种规律。
10.分数除法:
分数除法是分数乘法的逆运算。
11.分数除法计算法则:
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
12.分数除法的意义:
与整数除法的意义相同,都是已知两个因数的积与其中一个因数求另一个因数。
13.分数除法应用题:
先找单位1。单位1已知,求部分量或对应分率用乘法,求单位1用除法。
14.比和比例:
比和比例一直是学数学容易弄混的几大问题之一,其实它们之间的问题完全可以用一句话概括:比,等同于算式中等号左边的式子,是式子的一种(如:a:b);比例,由至少两个称为比的式子由等号连接而成,且这两个比的比值是相同(如:a:b=c:d)。
所以,比和比例的联系就可以说成是:比是比例的一部分;而比例是由至少两个比值相等的比组合而成的。表示两个比相等的式子叫做比例,是比的意义。比例有4项,前项后项各2个.
15.比的基本性质:
比的前项和后项都乘以或除以一个不为零的数。比值不变。
比的性质用于化简比。
比表示两个数相除;只有两个项:比的前项和后项。
比例是一个等式,表示两个比相等;有四个项:两个外项和两个内项。
16.比例的性质:
在比例里,两个外项的乘积等于两个内项的乘积。比例的性质用于解比例。
17.比和比例的区别
(1)意义、项数、各部分名称不同。比表示两个数相除;只有两个项:比的前项和后项。如:a:b 这是比 比例是一个等式,表示两个比相等;有四个项:两个外项和两个内项。 a:b=3:4 这是比例。
(2)比的基本性质和比例的基本性质意义不同、应用不同。比的性质:比的前项和后项都乘或除以一个不为零的数。比值不变。比例的性质:在比例里,两个外项的乘积等于两个内项的乘积相等。比例的性质用于解比例。* 比例是由两个相等的比组成。
18.比和比例的意义
比的意义是两个数的除又叫做两个数的比,而比例的意义是表示两个比相等的式子是叫做比例。比是表示两个数相除,有两项;比例是一个等式,表示两个比相等,有四项。因此,比和比例的意义也有所不同。而且,比号没有括号的含义 而另一种形式,分数有括号的含义!
19.比和比例的*
比和比例有着密切联系。比是研究两个量之间的关系,所以它有两项;比例是研究相关联的两种量中两组相对应数的关系,所以比例是由四项组成。比例是由比组成的,如果没有两种量的比,比例就不会存在。比例是比的发展,如果把比例式中右边的比看成一个数,比和比例此时又可以统一起来。
如果两个比相等,那么这两个比就可以组成比例。成比例的两个比的比值一定相等。
20.圆:
平面上到定点的距离等于定长的所有点组成的图形叫做圆。
21.圆心:
圆任意两条对称轴的交点为圆心。
注:圆心一般符号O表示
22.直径:
通过圆心,并且两端都在圆上的线段叫做圆的直径。直径一般用字母d表示。
23.半径:
连接圆心和圆上任意一点的线段,叫做圆的半径。半径一般用字母r表示。
圆的直径和半径都有无数条。圆是轴对称图形,每条直径所在的直线是圆的对称轴。在同圆或等圆中:直径是半径的2倍,半径是直径的二分之一。d=2r或r=d/2。
圆的半径或直径决定圆的大小,圆心决定圆的位置。
24.圆的周长:
围成圆的曲线的长度叫做圆的周长,用字母C表示。
25.圆周率:
圆的周长与直径的比值叫做圆周率。
圆的周长除以直径的商是一个固定的数,把它叫做圆周率,它是一个无限不循环小数(无理数),用字母π表示。计算时,通常取它的近似值,π≈3.14。
直径所对的圆周角是直角。90°的圆周角所对的弦是直径。
26.圆的面积公式:
圆所占平面的大小叫做圆的面积。πr^2;用字母S表示。
一条弧所对的圆周角是圆心角的二分之一。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等。
在同圆或等圆中,如果两条弧相等,那么他们所对的圆心角相等,所对的弦相等,所对的弦心距也相等。
27.周长计算公式
(1)已知直径:C=πd
(2)已知半径:C=2πr
(3)已知周长:D=c/π
(4)圆周长的一半:1/2周长(曲线)
(5)半圆的周长:1/2周长 直径(π÷2 1)
28.面积计算公式:
(1)已知半径:S=πr2
(2)已知直径:S=π(d/2)2
(3)已知周长:S=π[c÷(2π)]2
29.百分数与分数的区别
(1)意义不同。百分数是“表示一个数是另一个数的百分之几的数。”它只能表示两数之间的倍数关系,不能表示某一具体数量。因此,百分数后面不能带单位名称。分数是“把单位‘1’平均分成若干份,表示这样一份或几份的数”。分数还可以表示两数之间的倍数关系.
(2)应用范围不同。百分数在生产、工作和生活中,常用于调查、统计、分析与比较。而分数常常是在测量、计算中,得不到整数结果时使用。
(3)书写形式不同。百分数通常不写成分数形式,而采用百分号“%”来表示。因此,不论百分数的分子、分母之间有多少个公约数,都不约分;百分数的分子可以是自然数,也可以是小数。
而分数的分子只能是自然数,它的表示形式有:真分数、假分数、带分数,计算结果不是最简分数的一般要通过约分化成最简分数,是假分数的要化成带分数。任何一个百分数都可以写成分母是100的分数,而分母是100的分数并不都具有百分数的意义.
(4)百分数不能带单位名称;当分数表示具体数时可带单位名称。
30.百分数应用
百分数一般有三种情况:
①100%以上,如:增长率、增产率等。
②100%以下,如:发芽率、成长率等。
③刚好100%,如:正确率,合格率等。
31.百分数的意义
百分数只可以表示分率,而不能表示具体量,所以不能带单位。百分数概念的形成应以学生实际生活中的事例或工农业生产中的事例引入。
32.日常应用
每天在电视里的天气预报节目中,都会报出当天晚上和明天白天的天气状况、降水概率等,提示大家提前做好准备,就像今天的夜晚的降水概率是20%,明天白天有五~六级大风,降水概率是10%,早晚应增加衣服。20%、10%让人一目了然,既清楚又简练。
32.知识点扩展
1.圆的定义
几何说:平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径。
轨迹说:平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆。
集合说:到定点的距离等于定长的点的集合叫做圆。
2.圆弧和弦:圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧,半圆既不是优弧,也不是劣弧。连接圆上任意两点的线段叫做弦。圆中最长的弦为直径。
3.圆心角和圆周角:顶点在圆心上的角叫做圆心角。顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。
4.内心和外心:和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。
5.扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。圆锥侧面展开图是一个扇形。这个扇形的半径称为圆锥的母线。
6.圆的种类:(1)整体圆形,(2)弧形圆,(3)扁圆,(4)椭形圆,(5)缠丝圆,(6)螺旋圆,(7)圆中圆、圆外圆,(8)重圆,(9)横圆,(10)竖圆,(11)斜圆。
7.圆和其他图形的位置关系:圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,0≤PO