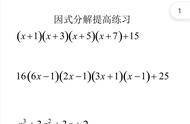2、完美的练习带来完美的结果

大量正确的训练,才能带来正确的结果。可是,我在教学中发现,很多学生在还没有熟练运用因式分解公式的时候,就开始大量快速练习,这可能会导致公式用混,还有各种层出不穷的错误。
如果我们一开始老是练习错误的方法。不好意思,错误的回路会变得非常强大,那你以后就总会在这里犯错。因此,用公式最最重要的是一定用对,这样我们的神经才会建立起越来越多正确回路。当不断地正确练习加粗神经回路,就相当于把它建成了高速公路,这时候你想不快都难!!!
因此核心要点是做正确!一开始可以慢,细细体会公式如何套用,通过不断地练习,高速路建好了自然会快起来,而且还很准确。
3、因式分解快速训练法
划重点:千万别死记硬背,不断地使用它,使用它,使用它!!!
训练方法:
1)每次写作业时,先把公式默写下来,先翻书确认写的对不对,不对马上修正。
2)把公式放在随时能看到的地方,做题时对照着公式来写题目。(考试时也可如此,先把公式默写下来)
3)开始做题,按如下方法思考。强调:整个过程都可以随时看你默写下来的公式。
这个式子能不能提公因式?
可以,先提出来。提出来后的有几项?
不可以,这个式子有几项?
两项都是平方项且相减→用平方差公式
三项且三项都同号→完全平方公式(A B)型
三项且中间项与平方项异号→完全平方公式(A-B)型
如果不符合完全平方公式怎么办?(A、B的关系和中间项对不上)用十字相乘法。
一开始训练,把细节写出来,别省步骤,刚开始慢,能有效地训练髓鞘化,让我们把任何一个细节都关注到,当逐渐熟悉,基本不出错的之后,再训练跳步骤。


4)看着公式来变形,不断地使用就会让公式越来越熟悉,这样训练,我们会慢慢体会到公式的变形要义,能够保证不用错公式。
如果能够每天做上15题,训练一周,你自然会看到变化~完全可以就地取材,在课本上选择题目,或者是从自己的家庭作业里选择。先保证做对,然后练习提速。
如果已经有一些错误的回路,修正方法还是类似的,用正确的方法来训练,直到正确方法的神经回路强于错误回路,这时候脑子就会自动走康庄大道啦~
以上主要说的是公式法的运用。关于因式分解十字相乘法,其实训练方法是一样的,只不过十字相乘会更加灵活,需要训练的是如何变化。我将在后面专门分享。
成功就是把复杂的问题简单化,然后狠狠去做。
欢迎关注圆周派讲数学,每天分享数学题目和学习方法,授人以鱼,亦授人以渔!