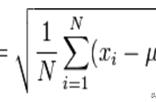第二十章 数据的分析
【学习目标】
1. 了解加权平均数的意义和求法,会求实际问题中一组数据的平均数,体会用样本平均数估计总体平均数的思想.
2. 了解中位数和众数的意义,掌握它们的求法.进一步理解平均数、中位数和众数所代表的不同的数据特征.
3. 了解极差和方差的意义和求法,体会它们刻画数据波动的不同特征.体会用样本方差估计总体方差的思想,掌握分析数据的思想和方法.
4. 从事收集、整理、描述和分析数据得出结论的统计活动,经历数据处理的基本过程,体验统计与生活的联系,感受统计在生活和生产中的作用,养成用数据说话的习惯和实事求是的科学态度.
【要点梳理】
要点一、算术平均数和加权平均数
一般地,对于个数,我们把叫做这个数的算术平均数,简称平均数,记作.计算公式为.
要点诠释:平均数表示一组数据的“平均水平”,反映了一组数据的集中趋势.
(1)当一组数据较大时,并且这些数据都在某一常数附近上、下波动时,一般选用简化计算公式.其中为新数据的平均数,为取定的接近这组数据的平均数的较“整”的数.
(2)平均数的大小与一组数据里的每个数据均有关系,其中任一数据的变动都会相应引起平均数的变动.所以平均数容易受到个别特殊值的影响.
若个数的权分别是,则叫做这个数的加权平均数.
要点诠释:(1)相同数据的个数叫做权,越大,表示的个数越多,“权”就越重. 数据的权能够反映数据的相对“重要程度”.
(2)加权平均数实际上是算术平均数的另一种表现形式,是平均数的简便运算.
要点二、中位数和众数
1.中位数的概念:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数称为这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数称为这组数据的中位数.
要点诠释:(1)一组数据的中位数是唯一的;一组数据的中位数不一定出现在这组数据中.
(2)由一组数据的中位数可以知道中位数以上和以下数据各占一半.
2.众数的概念:一组数据中出现次数最多的数据称为这组数据的众数.
要点诠释:(1)一组数据的众数一定出现在这组数据中;一组数据的众数可能不止一个;如果所有数据出现的次数都一样,那么这组数据就没有众数.
(2)众数是一组数据中出现次数最多的数据而不是数据出现的次数.
要点三、平均数、中位数与众数的联系与区别
*平均数、众数、中位数都是用来描述数据集中趋势的量,其中以平均数最为重要.
区别:平均数的大小与每一个数据都有关,任何一个数的波动都会引起平均数的波动,当一组数据中有个别数据太高或太低,用平均数来描述整体趋势则不合适,用中位数或众数则较合适.中位数与数据排列位置有关,个别数据的波动对中位数没影响;众数主要研究各数据出现的频数,当一组数据中不少数据多次重复出现时,可用众数来描述.
要点四、极差、方差和标准差
用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围,用这种方法得到的差称为极差,极差=最大值-最小值.
要点诠释:极差是最简单的一种度量数据波动情况的量,它受极端值的影响较大.一组数据极差越小,这组数据就越稳定.
方差是反映一组数据的整体波动大小的特征的量.要点诠释:(1)方差反映的是一组数据偏离平均值的情况.方差越大,数据的波动越大;方差越小,数据的波动越小.
(2)一组数据的每一个数都加上(或减去)同一个常数,所得的一组新数据的方差不变.
(3)一组数据的每个数据都变为原来的倍,则所得的一组新数据的方差变为原来的倍.
方差的算术平方根叫做这组数据的标准差,标准差的数量单位与原数据一致.
要点五、极差、方差和标准差的联系与区别
*极差与方差、标准差都是表示一组数据离散程度的特征数.
区别:极差表示一组数据波动范围的大小,它受极端数据的影响较大;方差反映了一组数据与其平均值的离散程度的大小.方差越大,稳定性也越小;反之,则稳定性越好.所以一般情况下只求一组数据的波动范围时用极差,在考虑到这组数据的稳定性时用方差.
要点六、用样本估计总体
在考察总体的平均水平或方差时,往往都是通过抽取样本,用样本的平均水平或方差近似估计得到总体的平均水平或方差.
要点诠释:(1)如果总体数量太多,或者从总体中抽取个体的试验带有破坏性,都应该抽取样本.取样必须具有尽可能大的代表性.
(2)用样本估计总体时,样本容量越大,样本对总体的估计也越精确.样本容量的确定既要考虑问题本身的需要,又要考虑实现的可能性所付出的代价.