三年级科学什么叫做浮力（小学三年级科学浮力与什么有关） - 原点资讯

三年级科学什么叫做浮力,小学三年级科学浮力与什么有关(1)

浮力是使船和沙滩球漂浮在水面上的力量。术语“ 浮力”是指流体（液体或气体）施加在部分或完全浸没在流体中的物体上的向上的力。浮力也解释了为什么我们可以比在陆地上更容易地将物体抬升到水下。

根据罗马建筑师维特鲁威（Vitruvius）的说法，希腊数学家和哲学家阿基米德（Archimedes）在公元前 3世纪首次发现了浮力，同时对锡拉丘兹国王希罗二世（Hiero II）提出的问题感到困惑。希罗国王怀疑他的金冠是用花圈制成的，实际上并不是纯金制成的，而是金银混合物。

据说，在洗澡时，阿基米德注意到他越沉入浴缸，水流出的越多。他意识到这是他的困境的答案，并在哭“Eureka！”时冲回家（“我找到了！”）然后他制作了两个物体 - 一个金币和一个银子 - 与皇冠的重量相同，然后将每一个放入装满水的边缘的容器中。

阿基米德观察到，银质量导致更多的水流出容器而不是黄金。接下来，他观察到他的“金”皇冠使得更多的水流出血管而不是他创造的纯金物体，即使这两个皇冠的重量相同。因此，阿基米德证明他的王冠确实含有银。

虽然这个故事说明了浮力的原理，但它可能是一个传说。阿基米德从未自己写过故事。此外，在实践中，如果确实将少量的银交换为黄金，则移位的水量太小而无法可靠地测量。

在发现浮力之前，人们认为物体的形状决定了它是否会漂浮。

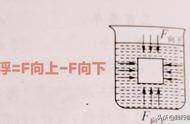
浮力来自静水压力的差异- 静态流体施加的压力。放置在流体中较高的球将比进一步向下放置的球经受更少的压力。这是因为当流体更深时，有更多的流体，因此更多的重量作用在球上。

因此，物体顶部的压力弱于底部的压力。可以使用公式Force = Pressure x Area将压力转换为力。有一个向上的净力。这种净力 - 无论物体的形状如何都指向上方 - 是浮力。

静水压力由P = rgh给出，其中r是流体的密度，g是由于重力引起的加速度，h是流体内的深度。静水压力不依赖于流体的形状。

所述阿基米德原理指出浮力施加被部分或完全浸没在流体中的物体上等于由对象移动的流体的重量。

这由公式F = rgV表示，其中r是流体的密度，g是由于重力引起的加速度，V是由物体移位的流体的体积。如果物体完全浸没，则V仅等于物体的体积。

浮力是向上的力，它抵抗向下的重力。浮力的大小决定了物体在浸没在流体中时是否会下沉，漂浮或上升。

还可以从公式中得出其他一些观察结果。

体积为2.0cm ^3的立方体浸没在水中。立方体经历的浮力是多少？

体积为2.0cm ^3的立方体完全浸没在水中。立方体经历的浮力是多少？

我们知道F = rgV。
r =水密度= 1000kg / m3
g =重力加速度= 9.8 m / s ²
V =立方体积= 2.0cm ³ = 2.0×10 ^-6 m 3
因此，F = 1000kg / m ³ *（9.8m / s ²）* 2.0×10 -6 m ³ = .0196（kg * m）/ s ²= 0.0196牛顿。

比耶洛，大卫。“事实还是虚构？：阿基米德创造了这个词'尤里卡！' 在巴斯。“ 科学美国人，2006年，https：//www.scientificamerican.com/article/fact-or-fiction-archimede/。
“密度，温度和盐度。” 夏威夷大学，https：//manoa.hawaii.edu/exploringourfluidearth/physical/density-effects/density-temperature-and-salinity。
罗瑞斯，克里斯。“金冠：简介。” 纽约州立大学，https：//www.math.nyu.edu/~crorres/Archimedes/Crown/CrownIntro.html。