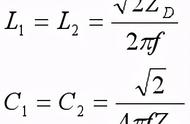图8:24dB林克威兹–瑞利高通和低通滤波器,在1.3KHz。注意相位响应的重合,所以蓝色相位图不可见
我们可以看到用了这些分频器件后的效果,以图5中所描述的系统为例,效果如图9中所示。

图 9:用1.3KHz 24dB 林克威兹–瑞利高通和低通滤波器代替图6 中的高通和低通滤波器处理后的图示,粉红色-低频,蓝色-高频,红色-总体。注意相位响应的不同。
图中曲线显示了和图6做一样处理的系统全频响应,不同的是这里将高通和低通滤波器替换为对称的分频点在1.3kHz的24dB林克威兹–瑞利滤波器。1.3kHz是图7中所描述的系统的分频点,所以这里采用1.3kHz作为分频点。
我们下面再来看一下其他两种可能,其一为消除在前一个例子中所说的设置中的延时,因为一些廉价的分频器不具有延时的调整,或无法做0.5ms的精细调整,图10展示了系统没有延时的效果。

图10:系统描述在图9中,没有延时
另一种值得考虑的方案是把对称的24dB林克威兹–瑞里滤波器的分频点设置在1.8kHz,这与图4中的电子滤波器的分频点是相同的,这将产生0.5ms的延时,结果如图11所示。

图11:系统显示在图10中,加上分频点设置到1.3KHz。红色-加0.5ms延时,绿色-没有延时。
最后,我们考虑在图9中使用对称的24dB林克威兹–瑞里滤波器的原例,这个系统需要固定一个外部的参数或图形均衡器,我们来具体研究怎样才能使系统的响应曲线变得平坦。