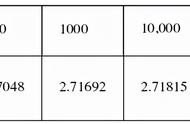
自然对数的导数是1/x,即d/dx ln(x) = 1/x
这个性质表明,自然对数是一个可微函数,并且其导函数可以用自然对数本身来表示。数学常数e是一个超越数,也就是说,它不是任何有理数(如整数、分数)的根。这个性质表明,数学常数e是一个非常特殊的数,它与其他任何有理数都存在本质区别。
3.2、自然对数和指数函数e^x是彼此的反函数,即ln(e^x) = x 和 e^(ln(x)) = x
这个性质表明,自然对数和指数函数是一对互逆的函数,它们可以相互转化和应用。
四、自然对数和数学常数e的应用自然对数和数学常数e在数学和物理中有着广泛的应用。例如:
4.1微积分中的微分和积分都可以用自然对数和指数函数表示。
例如,考虑一个函数f(x) = ln[x/(x^2 1)]。我们可以用微积分的方法求出f(x)的导函数为f'(x) = 1/(x^2 1)-2x/[x(x^2 1)]。一般情况下,f(x)的导函数无法用有限次的简单函数表示,但是如果我们将f(x)表示为f(x) = ln[x/(x^2 1)] = ln(x)-ln(x^2 1),则f(x)的导函数可以分别用自然对数和指数函数表示为:
f'(x) = d/dx [ln(x)] - d/dx [ln(x^2 1)]
= 1/x - 2x/(x^2 1)/(x^2 1)
= (x^2-1)/(x(x^2 1))^2
复变函数中的欧拉公式e^(iθ) = cos(θ) isin(θ)就涉及到了数学常数e和三角函数的关系。
欧拉公式是数学中非常重要的公式之一,它将指数函数、三角函数和虚数单位i联系在了一起。这个公式可以用泰勒级数的方法推导出来,即:

这个式子表明,三角函数和指数函数之间存在本质联系,而数学常数e是这种联系的一个重要因素。
4.2 概率论中的指数分布函数和泊松分布函数都涉及到了自然对数和指数函数。
在概率论中,指数分布函数和泊松分布函数是非常重要的分布函数。其中,指数分布函数表示等待时间在一个确定的时间内发生事件的概率分布,而泊松分布函数表示在一个单位时间内事件的发生次数的概率分布。这两个分布函数都可以用自然对数和指数函数来表示。

泊松分布
举例来说,考虑指数分布函数,其概率密度函数为:
f(x) = λe^(-λx)
其中λ是一个正常数。这个概率密度函数可以通过自然对数和指数函数来表示:
f(x) = λe^(-λx) = λe^(ln[e^(-λx)])
= λe^(-λx)*e^(ln(λ))

4.3 物理中的放射性衰变、振荡电路等现象都可以用自然对数和指数函数来描述。
在物理中,放射性衰变、振荡电路等现象都涉及到了自然对数和指数函数。
举例来说,考虑一个放射性样品,其衰变速率随时间的变化规律可以用指数函数表示。假设该样品初始时刻的放射性核数为N0,其衰变速率为λ,则在任意时刻t,其放射性核数N(t)与初始时刻的核数N0的比值可以用自然对数和指数函数表示:
N(t)/N0 = e^(-λ*t)
这个式子表明,在任意时刻t,放射性核数与初始时刻的核数N0的比值是一个以指数函数衰减的形式变化的。
结语自然对数和数学常数e是数学中至关重要的概念,它们不仅具有理论上的意义,而且具有广泛的实际应用。通过了解自然对数和数学常数e的定义、性质和应用,可以扩展我们的数学知识,提高数学应用能力,进一步认识数学在各行各业中的重要作用。
想了解更多精彩内容,快来关注闻讯百通