52=2.69(元)。
从中不难看出,一年之中这样的存取时间越短(存取次数越多)收益越多。由此,许多人会产生如下自然问题:既然一年中存取的次数越多越合算,而且银行规则允许,那就不嫌麻烦反复存取,甚至都可以想象成坐在银行取款台那里不走,拿了就存然后再取再存(存取间隔以秒计),如此反复操作,储户是不是能以小博大得到巨额本息?(这正是伯努利提出的复利问题:假设n为利息复利的次数,利率是其倒数,一年后的收益为(1 )n,那么,n如果变得无限大,那(1 )n是否也会变得无限大?)为了解开大家的疑惑,可作以下具体说明:
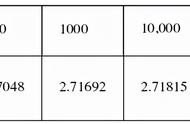
把1元在一年中分成n次存取,那么你会得到(1+)×(1+)×…×(1+)=(1+)n(元)本息,因为结果一共是n项的乘积,显然,当n取无穷大时,结果就是你最多能得到的钱数。

图源:goolge.com
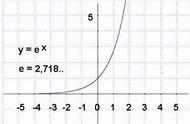
数学大师欧拉经过研究给出明确结果:当n趋于无穷大时,(1 )n=2.718281828459……并于1727年首次用小写字母“e”表示这个常数,以后逐渐成为标准,被称为自然常数。
也就是说,1元本金无论存取多少次,极限值为e≈2.718281828……(元)。除去本金1元,一年内总利息最多仅为1.7183元左右。如此一来,数学家严谨的分析给银行家吃了颗定心丸,难怪人们戏称e是银行家最喜欢的一个数,同时证实大家想当然的想象只不过是多余的担忧。
在数学中关于常数e的定义,最常见的有如下两种:
⑴定义e为一个数列的极限值:e=

⑵定义e为下列无穷级数之和:e=