摘要:正多面体是一种具有特定形状和性质的几何体。在数学中,正多面体是一种特殊的多面体,它的每个面都是一个完全相同的正多边形。本文将详细探讨为什么正多面体只有5种,并解释这个结果背后的数学原理和思想。
一、引言
正多面体是一种具有特定形状和性质的几何体。在数学中,正多面体是一种特殊的多面体,它的每个面都是一个完全相同的正多边形。正多面体的种类非常有限,只有5种。这个结果在数学中具有重要的意义,因为它揭示了正多面体的本质特征和规律。本文将详细探讨为什么正多面体只有5种,并解释这个结果背后的数学原理和思想。
二、正多面体的定义与性质
正多面体是一种特殊的多面体,它的每个面都是一个完全相同的正多边形。正多边形的定义是一个多边形,它的所有边和角都相等。因此,正多面体的所有面都是完全相同的正多边形。
正多面体具有一些重要的性质。首先,正多面体的所有边都相等。其次,正多面体的所有角都相等。最后,正多面体的所有面的面积都相等。这些性质使得正多面体具有独特的形状和性质。

三、正多面体的种类
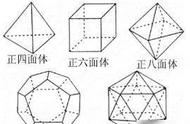
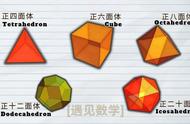
根据上述性质,我们可以推断出正多面体的种类非常有限。事实上,数学家们已经证明了正多面体只有5种:正四面体、正六面体、正八面体、正十二面体和正二十面体。这些正多面体都具有独特的形状和性质,它们在几何学和物理学等领域中具有重要的应用价值。
四、为什么正多面体只有5种
为什么正多面体只有5种呢?这个问题涉及到几何学和数学的深层次原理。首先,我们要明白一个基本事实:一个正多边形的内角是固定的,这个角度取决于它的边数。例如,一个正三角形的内角是60°,一个正方形的内角是90°,一个正五边形的内角是108°等等。
其次,当我们将这些正多边形组合成一个多面体时,每个面的内角之和必须等于360°。这是因为一个封闭的多边形(如球)的内角之和总是360°。因此,我们可以通过调整不同正多边形的数量来得到不同的正多面体。
通过观察和实践,我们可以发现只有5种不同的方式可以组合这些正多边形以满足上述条件:
- 正四面体:由4个正三角形组成。
- 正六面体:由6个正方形组成。
- 正八面体:由8个正五边形组成。
- 正十二面体:由12个正五边形组成。
- 正二十面体:由20个正三角形组成。
这就是为什么正多面体只有5种的原因。这个结果不仅揭示了正多面体的本质特征和规律,也展示了数学在几何学中的重要应用价值。
五、结论与思考
通过探讨为什么正多面体只有5种,我们不仅理解了这一数学问题的本质和原理,也揭示了数学在几何学中的重要应用价值。这个结果提醒我们,数学不仅是抽象的学问,它也可以帮助我们理解和解释现实世界中的各种现象和规律。同时,这个结果也展示了数学的严谨性和逻辑性,它使我们能够通过推理和证明来验证和确认我们的结论和假设。
此外,这个结果也提醒我们要保持开放的心态和好奇心,不断探索和学习新的知识和领域。只有这样,我们才能更好地理解和应用数学,为科学和社会的发展做出更大的贡献。
,