我们都学习过导数,对于普通数学爱好者而言,可以说导数就是区分初等数学和高等数学的分界岭。今天我们就来聊聊到底什么是导数,基本初等函数都是如何求导的?
函数y=f(x)在点x=x0的导数就是指函数图像在点x0处的切线的斜率k,记作k=y′(x0)=f′(x0)。
那我们怎么来求出这个切线的斜率呢?我们首先在函数图像上取两点
P0(x0,y0)和P(x0 △x,y0 △y)
这里y0=f(x0),y0 △y=f(x0 △x)
△y=f(x0 △x)-y0=f(x0 △x)-f(x0)
连接直线P0P,这里P0P就是函数图像的一条割线。当△x→0的时,x0 △x→x0,点P也就逐渐趋近于点P0,割线P0P趋近于过点P0的切线,割线P0P的斜率也就趋近于这条切线的斜率。这个过程的极限值就是函数在点x0的导数。

割线P0P的斜率等于
[(y0 △y)-y0]/[(x0 △y)-x0]
=△y/△x
过点P0的切线的斜率
k=y′(x0)=f′(x0)
=lim(△y/△x),△x→0
=lim{[f(x0 △x)-f(x0)]/△x}
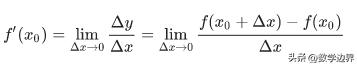
函数y=f(x)在定义域内每一个点的导数所构成的函数称为函数的导函数,记为y′=f′(x)。
y′=y′(x)=f′(x)=lim(△y/△x)
=lim{[f(x △x)-f(x)]/△x},△x→0

我们把自变量x的增量△x用dx表示,称为自变量的微分;把因变量y的增量△y用dy表示,称为因变量的微分。那么导函数又可以表示为:
y′=y′(x)=f′(x)=dy/dx,dy=f′(x)dx