八进制转十进制 (除0以外,任何数的0次方都是1)
按权相加法。(将八进制每位上的数乘以位权,将得出来的数再加在一起)。
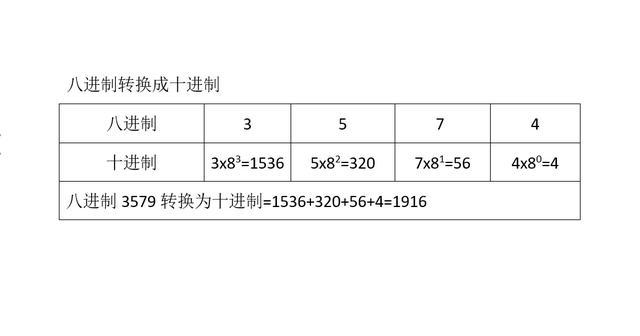
例如:八进制3574转十进制:
4*8的0次方=4*1=4(除0以外,任何数的0次方都是1)
7*8的1次方=7*8=56
5*8的2次方=5*8*8=320
3*8的3次方=3*8*8*8=1536
所以八进制3574转为十进制=1536 320 56 4=1926
例如:八进制1111转十进制:
1*8的0次方=1*1=1(除0以外,任何数的0次方都是1)
1*8的1次方=1*8=8
1*8的2次方=1*8*8=64
1*8的3次方=1*8*8*8=512
所以八进制1111转为十进制=512 64 8 1=585
例如:八进制11.11转十进制:
(整数部分从0次方开始,次方从右往左0,1,2...
小数部分从负的1次方开始,次方从左往右-1,-2,-3...)
一个数的-x次方,就是一个数的x次方的倒数,也就是它的x次方分之一
所以八的负一次方等于八的一次方分之一,也就等于八分之一
8⁻¹=1/8¹=1/8=0.125
8⁻²=1/8²=1/64=0.015625
整数部分:
1*8的0次方=1*1=1(除0以外,任何数的0次方都是1)
1*8的1次方=1*8=8
小数部分
1*8的-1次方=1*8⁻¹=1/8¹=1/8=0.125
1*8的-2次方=1*8⁻²=1/8²=1/64=0.015625
所以八进制11.11转为十进制=1 8 0.125 0.015625=9.140625
十进制转八进制方法(分为整数部分和小数部分)
整数部分:每次将整数部分除以8,余数为该位权上的数,商继续除以8,以此类推,直到商为零,从最后一个余数向前排列就可以了。我们称这种方法为除8取余法。
(用十进制除以8,除的断的整数,用0表示; 除不断的,大于等于1的,用余数表示,余数为该位权上的数;直到商为零,从最后一个余数向前排列就可以了。)

例如:十进制168的八进制,168/8
168/8=21,除的断的整数,用0表示——0
21/8=2.625.....21-2*8=5,余5,除不断的,大于等于1的,用余数表示——5
2/8=0.25......余2,直到商为零,从最后一个余数向前排列——2
所以十进制168的八进制为250
例如:十进制169的八进制,169/8
169/8=21.1......169-21*8=1,余1,除不断的,大于等于1的,用余数表示——1
21/8=2.625.....21-2*8=5,余5,除不断的,大于等于1的,用余数表示——5
2/8=0.25......余2,直到商为零,从最后一个余数向前排列——2
所以十进制169的八进制为251
例如:十进制111的八进制,111/8
111/8=13.875......111-13*8=7,余7,除不断的,大于等于1的,用余数表示——7
13/8=1.625.....13-1*8=5,余5,除不断的,大于等于1的,用余数表示——5
1/8=0.125......余1,直到商为零,从最后一个余数向前排列——1
所以十进制111的八进制为157
例如:十进制10的八进制,10/8
10/8=1.25......10-1*8=2,余2,除不断的,大于等于1的,用余数表示——2
1/8=0.125......余1,直到商为零,从最后一个余数向前排列——1
所以十进制10的八进制为12
例如:十进制8的八进制,8/8
8/8=1,除的断的整数,用0表示——0
1/8=0.125......余1,直到商为零,从最后一个余数向前排列——1
所以十进制8的八进制为10