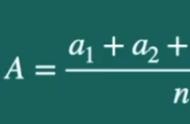今天给大家介绍的是统计学中的一个基本概念——数学期望。
这个名字乍一看着实很古怪,数学?哦,太可怕了。期望?这又是个啥,期望啥,期望今天中午能吃到周黑鸭吗?
哈哈,虽然听起来很古怪,但“数学期望”这个概念,实际上衡量的就是“事物的平均水平”。
那我们能不能说,数学期望就是平均数呢?数学期望就是均值呢?
答案是,既可以这么说,但又不完全能这么说。

让我们来看两个小例子:
第一个例子,某个班有5个小朋友。
他们这一次语文考试的成绩是70分、80分、85分、90分和100分,
那么此时,这个班级考试成绩的数学期望是多少呢?
很简单,此时数学期望就等于平均数,也就是85分。

第二个例子,小明班里明天要去野餐,他问老妈要钱。
老妈赢了麻将,心情不错时,会给他200块钱;心情一般,那就给他100块钱;要是输了麻将,心情奇差无比,那么可怜的小明就只能拿到可怜的50块钱。
今天一进门,小明就通过自己惊人的洞察力,从老妈的脸色中观察出,今天老妈心情不错的概率是2/3,心情一般的概率是1/3,心情很差的概率为0,
那么请问,今天小明能拿到多少钱呢?
或者说,小明能拿到的钱的数学期望是多少呢?
答案是:我们需要将小明可能拿到的钱分别乘以这些钱出现的可能性大小,最终答案是183.33元。

此时,聪明的你,一定能够发现了,数学期望描述的正是这样一种“带有不确定性的平均水平”。
实际上,小明最后只可能拿到“200元”或“150元”,又或者只有“可怜的50元”。
但考虑到这些结果发生的可能性大小,我们为了给出一个综合性的、平均而言的判断。
就需要考虑这些结果发生的可能性大小,最终得到这么一个“期望中的综合了所有可能情况后的平均结果”,也就是看起来有些古怪的“183.33元”。
我们再回过头去看第一个例子。
此时,要如何理解第一个例子中的数学期望85分呢,你可能会有疑问,因为确实有个小朋友考了85分呀,而且每个小朋友的考试成绩都是确定的,可能性都是100%,答案不应该是425分吗?

但这是不对的,因为这时候各种分数发生的可能性,并不是通常所认为的1(分数已经被老师批改出来了,已经确定了),而是1/5。
我们不妨这么理解,把所有小朋友的考试分数分别写在5张小卡片上,将它们扔到一个黑色的纸盒子里,老师从里面随机抽取一张卡片,记录下卡片上的分数。
那么这个被记录下来的分数的数学期望是多少呢?
很明显,抽到5张小卡片的概率各占了1/5,每一个分数被记录下来的可能性也就各占1/5,因此数学期望就是:

此时的数学期望,就相当于我们熟悉的算平均分,所以说,算平均分的过程,虽然看似一切都是确定的,但实际上也蕴含了不确定性,是"综合了所有可能情况后的平均结果”,只不过每种情况发生的可能性都等于(1/总人数)而已。
通过今天的小短文,大家有没有更了解数学期望了呢?
其实我们每天都会碰到各种各样的“数学期望”哦,每周的平均睡眠时间(可能性各占1/7)、王者荣耀里的中路位置综合得分等等,快去发现吧!
,