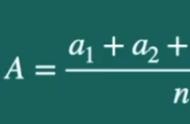所谓平均值法,就是形如a b=2m常数2m (或者a-b=m),取2m的一半m.
a b=2m a-m=m-b=t a=m t b=m-t
这样就通过一个变量t和a b的平均值m,使得a.b通过m t表示!
下面通过实际例题来讲讲运用.

先将4平分到两边:a-b=4=>a-2=b 2=t
a=t 2 b=t-2
(t 2)(t-2) cc 4=0
tt cc=0 t=c=0
a=2 b=-2
a b c=0
是不是非常简单,方便?简洁明了?[来看我]
下面再讲讲在求最大值(最小值)中的运用!
已知3x 4y=12 求xy的最大值.
一般情况下,学渣的思路是消元,用x表示y .y=(12-3x)/4
xy=x(12-3x)/4,再配方,求最大值。这种方法,不能说不对,就是太浪费时间!非常繁琐!
下面,我们来看看平均值法的妙用!
3x=6 t 4y=6-t
12xy=36-tt<=36
xy<=3 (t=0的时候取等号),是不是非常简单明了直观,省时省力?
有时候,韦达定理也可以和平均值法结合起来,起到不错的效果!
[来看我]已知a>0,b>0 a b=2,求证
aabb(aa bb)<=2
a-1=1-b=t a=2 t b=1-t (-1<t<1)
aabb(aa bb)=(1-tt)^2*2tt<=2
,