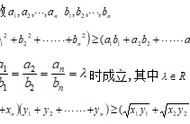知识无价,关注点赞
柯西(Cauchy,Augustin-Louis,1789-1857)是法国数学家、力学家。27岁成为巴黎综合工科学校教授,并当选为法国科学院 院士. 他的一生获得了多项重要的成果。柯西不等式便是他的一个非常重要的成果。除此之外他在数学的很多领域都进行了深刻的研究,其中包括数论、代数、数学分析和微分方程等,为数学的发展做出的突出的贡献。柯西对高等数学的贡献包括:无穷级数的敛散性,实变和复变函数论,微分方程,行列式,概率和数理方程等方面的研究.目前我们所学的极限和连续性的定义,导数的定义,以及微分、定积分用无穷多个无穷小的和的极限定义,实质上都是柯西给出的。数学中很多定理都冠以柯西的名字,如柯西收敛原理、柯西中值定理、柯西积分不等式、柯西判别法、柯西方程等等。

柯西
柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲,该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式,因为,正是后两位数学家(布涅柯夫斯基和施瓦茨)彼此独立地在积分学中推而广之,才将这一不等式应用到近乎完善的地步。 柯西不等式非常重要,而且形式优美,结构巧妙,他也是高中四大经典不等式(均值不等式、柯西不等式、排序不等式、切比雪夫不等式)之一,做为高中数学选修4-5的重要内容,灵活巧妙地应用它,可以使一些较为困难的问题迎刃而解在高考中拿分迅速准确。 柯西不等式在证明不等式、解三角形、求函数最值、解方程等问题的方面有很强大的应用。柯西不等式不仅在高等数学中是一个十分重要的不等式,而且它对初等数学也有很可的指导作用,利用它能高远瞩、居高临下,从而方便地解决一些中学数学中的有关问题。
一、柯西不等式的各种形式及其证明

一般形式及推论