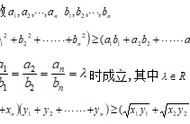先在柯西不等式的基础上把不等式构造出来,然后在进行求解。
由于许多式子的结构满足柯西不等式取等号的条件,因此可以利用不等式来解决等式的一些问题。例如下面的例题是一个三元二次方程组,依常规看,好像少了一个方程,但运用柯西不等式却可化腐朽为神奇,柳暗花明,让我们领悟到数学的奇异美。


柯西不等式结构对称和谐,具有较强的应用性,深受人们的喜爱。它作为一个基本而又重要的不等式,在数学领域中具有一定的地位。它不仅在高等数学中是一个重要的不等式,而且它对于初等数学的学习也有很大的指导意义。灵活巧妙地运用柯西不等式能高瞻远瞩,方便地解决初等和高等数学的有关问题,从而加深知识的理解与巩固。
能否熟练地应用就要看我们是否有去用它的意识,而且能否掌握其中的技巧,如果我们具备了就会使复杂问题简化,解题更加方便,快捷,收到事半功倍的效果。如何应用柯西不等式,难点在于构造,既要针对柯西不等式两端的形式,又要考虑问题所给条件和结论的内在联系,探索构造信息,有助于开阔眼界,培养思维的深刻性与发散性。其实对于数学上其它的公式、定理使用时也是如此,那就是:变形改造已知式,使定理公式的使用更便于结论的导出;创设、构造条件使看似不能利用相关定理、公式成为可能。
,