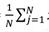很多嵌入式系统都需要通过A/D转换方式采集模拟信号,当干扰作用于模拟信号之后,A/D转换结果就会偏离真实值。如果仅采样一次,是无法确定该结果是否可信的,必须多次采样,得到一个A/D转换的数据系列,通过某种处理后,才能得到一个可信度较髙的结果这种用软件算法从采样数据(数据样品)系列中提取逼近真值数据的方法,通常称为数字滤波。数字滤波有硬件滤波的功效,却节省了硬件投资。实现数字滤波功能的软件算法称为数字滤波算法,由于数字滤波算法的灵活性,其效果往往是硬件滤波电路达不到的。
数字滤波的不足之处就是需要消耗一定的CPU机时,在进行实时信号处理时必须充分考虑到这一点。当有用信号为高频信号,干扰信号为低频信号时,需要采用髙通滤波。而实时髙通滤波算法受到CPU速度的限制,往往力不从心,而硬件高通滤波器却很容易处理这种实时信号。当有用信号为低频信号(如温度、湿度、重量、水位等等),其频串通常很低(甚至接近0.001 Hz),而干扰信号频率相对较髙时(如各种电磁干扰),需要采用低通滤波。由于硬件低通滤波器往往体积比较大,与当前电子产品微型化趋势不相容。而当前CPU的速度在执行实时低通滤波算法时完全可以胜任,故数字滤波主要应用领域为实时低通滤波。在某些情况下,数字滤波也用来进行带通滤波。
对于非实时信息处理,由于不受处理速度的制约,数字滤波算法广泛应用于各种音频数据、图片数据和视頻数据的加工处理。
如果用硬件手段(FPGA/CPLD)来实现数字滤波,其处理速度将有质的飞跃,滤波算法采用数学丁.具软件MATLAB来设计,滤波功能也将更加丰富多彩,应用频率范围也大大扩展。本章只介绍在嵌入式系统中广泛使用的几种数字滤波算法,这些算法都是用软件进行实时低频信号处理,达到提高系统抗干扰能力的目的。
常用的数字滤波算法有以下几种:
1) 程序判断滤波 2) 中值滤波 3) 算术平均滤波 4) 去极值平均滤波 5) 滑动平均滤波
6) 滑动加权滤波 7) 一阶滞后滤波
程序判断滤波本质上是低通滤波,由于毛刺型突发干扰为高频干扰,故可以被很好地滤除。另一方面,程序判断滤波采用限幅手段来达到滤波目的,对于幅度比较小的噪声干扰无能为力,即不能滤除随机干扰,因而只能用于对精度要求不是很髙的场合。
中值滤波本质上也是低通滤波,由于毛刺型突发干扰为髙频干扰,故可以被很好地滤除。由于中值滤波进行N次采样才输出一次有效值(即采样输出比N:1),抗突发干扰能力比程序判断滤波要提高很多,能够在干扰比较频繁的场合正常工作。另外,在N个数据样本中,中值样本通常受到的噪声干扰也比较小,故中值滤波箅法也具备一定的抗随机干扰能力(其能力与N正相关)。
中值滤波的效果虽然比程序判断滤波提高很多,但必须满足主采样周期远大于子采样周期的条件。而子采样周期受到毛刺型突发干扰持续时间的限制不能太短,故主采样周期必然较长,即被检测物理最的基波频率一定比较低(慢变信号),其应用场合受到一定的限制。
算术平均滤波对随机干扰的抑制效果与连续采样次数N密切相关,当采样次数N增加到一定程度后,被测物理量本身产生的变化量就会超过允许范围,再也不能忽略不计了。因此,连续采样次数N是不能任意增加的。其应用场合与中值滤波的应用场合类似,必须满足主采样周期远大于子采样周期的条件。而子采样周期受到毛刺型突发干扰持续时间的限制不能太短,故主采样周期必然较长,即被检测物理量的基波频率一定比较低(慢变信号),其应用场合受到一定的限制。
虽然算术平均滤波对随机干扰的抑制效果比较好,但却不能消除毛刺型突发干扰。只要有一个采样数据样本受到毛刺型突发干扰,算术平均值将明显偏离真实值,真是所谓“一粒老鼠屎坏了一锅汤”。
去极值平均滤波同时具有淸除毛刺型突发干扰和噪声型随机干扰的能力,在低频信号采集系统中被广泛采用。在各种文艺表演大赛的评奖计分中,经常听到主持人宜布“去掉一个最高分,去掉一个最低分,某某最终得分是9.73分”,这实际上就是采用去极值平均滤波算法。其中最髙分和最低分分别是“偏心眼”评委和“有成见”评委给出的(相当于毛刺型干扰),其他评委虽然“客观”地给分,但由于审美角度的差异,给出的分数也会有差异(相当于噪声型干扰),经过平均处理后,最终得分就能够比较客观地反映该演艺人员的真实水平。
如果连续N次采样中没有受到毛刺型干扰的数据样品,被剔除的将是两个随机误差最大的数据样品,滤波效果仍然很好。去极值平均滤波算法也有效果不佳的时候,如果连续N次采样中有两个以上的正毛刺数据样品或者两个以上的负毛刺数据样品,将至少有一个毛刺数据样品不能剔除,最终平均值必然与真实值存在明显偏差。
去极值平均滤波的应用条件与算术平均滤波的应用条件相同,主要用来对低频信号进行软件滤波。
,