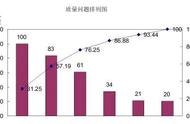
9.散布图
【定义】
把互相有关联的对应数据,在方格纸上以纵轴表示结果,以横轴表示原因;然后用点表示出分布形态,根据分布的形态来判断对应数据之间的相互关系。
【用途说明】
1.检定两变数间的相关性。
2.从特性要求寻找最适要因。
3.从要因预估特性水准。
【成对数据的对应关系】

【目的】
- 知道两组数据(或原因与结果)之间是否有相关及相关程度。
- 依据各种可能影响原因层别绘制散布图,可找出最适的要因。
- 检视是否为不相关。
【制作步骤】
- 收集相对应数据,至少30组以上,并且整理写到数据表上。
- 找出数据之中的最大值和最小值。
- 画出纵轴与横轴刻度,计算组距。
- 将各组对数据标示在座标上。
- 记录必要事项。
【范例:身高与体重散布图】

判读:

10.直方图
【定义】
将所收集的数据、特性值或结果值,在横轴上适当地区分成几个相等区间,并将各区间内测定值所出现的次数累加起来,用柱形画出的图形。
【使用目的】
1.测知制程能力。
2.测知数据的真伪。
3.测知分配型态。
4.计算产品不良率。
5.调查是否混入两个以上的不同群体。
6.藉以制定规格界限。
7.规格与标准值比较。
8.设计管制界限是否可用于制程管制。
9.求分配的平均值与标准差。
【制作步骤】
1.收集数据并且记录在纸上。
2.找出全体数据中之最大值(L)与最小值(S)
3.定全距(R)=最大值(L)-最小值(S)
4. 决定组数
——史特吉斯公式组数:K=1+3.32log n
n=数据个数
——组数决定参考表(经验法则)