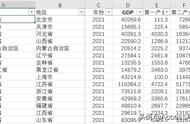
先说一个直观的结论:边长3微米的10^12维正方体无法塞进一个半径1米的10^12维球体之中
这源于一个很简单的计算:n维单位球体可以容纳的最大正方体边长等于
这并不是因为球体在变得狭窄,球体总是圆润的,实际上是随着维度的增高,正方体变得越来越多刺;就拿边长为2米的正方体举例,当n=2时因为它是正方形,所以它的最远点距离中点 米;当n=3时,立方体的最远点距离中点 米;……;等到n增加到 ,一个 维的正方体,哪怕边长仍然是2米,它的对角线长度已经跨越了两光年,因此此时拿一个半径一光年的球都不足以遮住它的刺
前段时间在知乎别的问题下看到的
一维单位球体(线段)的长度是2
二维单位球体(圆)的面积是π
三维单位球体的体积是4/3π
可以进行推广,称n维单位球体为满足(x1)²+...+(xn)²≤1的点全体构成的集合
如果对n维单位球体测量体积,会发现随着n趋于无穷大,球体的体积趋于0
感觉好像有人误解了什么,稍微补充一下。这里并不是球体与外切立方体体积比值那么简单
单位正方体的定义是边长为1,而单位球定义是半径为1,直径为2,因此二者是彼此穿插的,并非一者嵌入另一者之内
单位球的外接正方体是边长为2的正方体,体积为2^n,因此即便单位球与外接正方体的体积比例趋于0也不能说明单位球的体积趋于0
还有,很多人跟我说单位不同无法比较。比如边长1分米的正方体,如果把单位换算为米,则随着n的增大分别是0.1米,0.01平方米,0.001立方米,...,数值趋于0;而如果把单位换算为厘米,则随着n的增大分别是10厘米,100平方厘米,1000平方厘米,...,数值趋于无穷大;
但是,球体有着本质的一点区别:
不论你使用什么样的单位,球体的体积数值永远趋于0
,换一个角度说,就是无论你指定一个多么小的 ,总会有一个足够大的n,使得边长 的n维正方体体积超过n维单位球体的体积(这个结论比前一个结论强)
最后再说个无聊的……
√2是整数
这是因为代数学里有一个名词叫作“代数整数”,并且“代数整数”可以简称为“整数”
所谓代数整数就是整数环上首一多项式的根,√2是x²-2=0的根,因此是代数整数,也就是整数
没错,这只是个无聊的文字游戏而已