什么是加法交换律和乘法交换律

简介：

在两个数的加法运算中，在从左往右算的顺序，两个加数相加，交换加数的位置，和不变。此定律为小学四年级的学习内容。

公式：

a b=b a

定义：

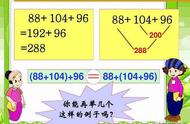
三个数相加，先把前两个数相加，再加另一个加数；或者先把后两个数相加，再加另一个加数，但和不变。

法则：

a b c=a (b c)=(a c) b

三个数相加，先把前两个数相加，或者先把后两个数相加。

例题

78 56 44=78 （56 44）=78 100=178

三个数相乘，先把前两个数相乘，或先把后两个数相乘，再和第三个数相乘，它们的积不变。它是一种简算定律，在小学四年级均有涉及。乘法交换律是乘法运算的一种运算定律。主要公式为ab=ba（注意，在乘法与数字中，乘号用·表示，列：a·b=b·a或：ab=ba）。

作用：

它可以改变乘法运算当中的运算顺序，在日常生活中乘法交换律运用的不是很多，主要是在一些较复杂的运算中起到简便的作用。

应用：

（1）因数中间有零或者未尾有零交换位置相乘一般情况下可以简便计算过程。

（2）其中一个因数由重复的数字组成的，利用交换律计算也有简便。

　　运算例题

如： 3×4×5=3×5×4=60

5.5×9×10=5.5×10×9=55×9=495

定义：三个数相乘，先把前两个数相乘，或先把后两个数相乘，积不变。

运算方法：

主要公式为(a×b)×c=a×(b×c)，它可以改变乘法运算当中的运算顺序 .在日常生活中乘法结合律运用的不是很多，主要是在一些较复杂的运算中起到简便的作用。

乘法结合律是三个数相乘，先把前两个数相乘，或先把后两个数相乘，积不变。

注意：乘法结合律不适用于向量的计算。例子：

69×125×8

=69×(125×8)

=69×1000

=6900

两个数相加(或相减)再乘另一个数，等于把这个数分别同两个加数（减数）相乘，再把两个积相加（相减），得数不变。

用字母表示：

（a b）x c=axc bxc

还有一种表示法：

ax(b c)=ab ac

示例

25×404

=25×(400 4)

=25×400 25×4

=10000 100

=10100

乘法分配律的逆运用

25×37 25×3

=25×(37 3)

=25×40

=1000

乘法分配律还可以用在小数、分数的计算上。

例题：

25×1.5 25 ×0.5

=25×(1.5 0.5)

=25×2

=50

同分母的分数相加减，只把分子相加减，分母不变。异分母的分数相加减，先通分，然后再加减。

分数乘法

分数乘整数

分数乘整数，用分数的分子和整数相乘的积做分子，分母不变。能约分（化简）的要约分（化简)。

例1：4/5×3=4×3/5=12/5

例2：3/22×2=3×2/22=6/22=3/11

分数乘分数

分数乘分数，用分子相乘的积做分子，分母相乘的积做分母。能约分（化简）的要约分（化简）。

例1：5/6×1/3=5×1/6×3=5/18

例2：2/5×1/4=2×1/5×4=2/20=1/10

分数除以整数（1）

分数除以整数，分母不变，如果分子是整数的倍数，则用分子除以整数，最后不是最简分数要化成最简分数。

例1：4/15÷2=4÷2/15=2/15

例2：42/30÷7=42÷7/30=6/30=1/5

分数除以整数（2）

分数除以整数，分母不变，如果分子不是整数的倍数，则用这个分数乘这个整数的倒数，最后不是最简分数要化成最简分数。

例1：3/8÷2=3/8×1/2=3×1/8×2=3/16

例2：4/5÷6=4/5×1/6=4×1/5×6=4/30=2/15

分数除以分数

分数除以分数，等于被除数乘除数的倒数，最后不是最简分数要化成最简分数。

例1：2/3÷3/4=2/3×4/3=2×4/3×3=8/9

例2：2/15÷1/3=2/15×3=2×3/15=6/15=2/5