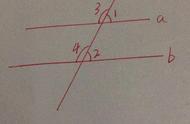及其判定
1、 :平面内,两条不相交的直线。
用“∥”表示,如:AB∥CD
2、平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
3、推论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
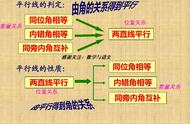
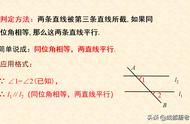
判定方法1、两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简写成:同位角相等,两直线平行。
判定方法2、两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简写成:内错角相等,两直线平行。
判定方法3、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简写成:同旁内角互补,两直线平行
例1、如图,∠1=∠3时,直线a与b平行吗?
当∠2 ∠3=180°,直线a与b平行吗?
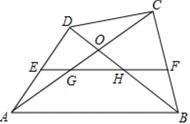
例2、直线AB、CD被直线EF所截,∠1=∠2,∠CNF ∠AME=180°。
说明AB∥CD MP∥NQ


解析:例1、∠1与∠4是对顶角,所以∠1=∠4;∠1=∠3,即∠4=∠3.所以a∥b。
∠2 ∠3=180°,∠2 ∠4=180°,即∠4=∠3.所以a∥b,出发点的对顶角和补角。
例2、∠CNF ∠AME=180°,∠CNF ∠CNE=180°,∠AME=∠CNE,则AB∥CD
∠ AME=∠CNE,∠AME=∠1 ∠6,∠CNE=∠2 ∠7,则∠6=∠7,所以MP∥NQ
,