正弦曲线长度计算公式,正弦曲线面积计算公式

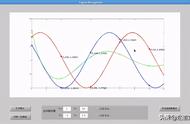
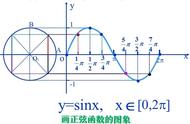
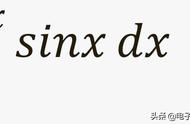正弦曲线的原方程：

性质：当一个圆的半径为1时，周长为：C=2πR=πd=2×π=2π，弧度与度之间的换算关系：

弧度=360o，弧长的计算公式为：L=（2πR/360）*α（α为圆心角），可以看出，当α=360o时，弧长L=圆的周长C=2πR=正弦曲线的直线长度，α=2π=360o，π=180o，π/2=90o=1，即等于圆的半径，X轴的坐标点为1，2π=360o，π=180o，X轴的坐标点为0。现在，我们把公式转化成数控车床坐标系：X=SINα，根据图4-40，圆的半径R=10，X轴的坐标为：X=R SIN（α/n），Z轴的坐标为：Z=2πR/n

十三、余弦曲线 X=COSα

余弦函数的图像叫做余弦曲线。

余弦曲线的原方程：X=COSα

从图像中可以看出，余弦曲线与正弦曲线的起点不同，由sin90o=cos0o=1，它们之间的差别为90o，现在，我们把公式转化成数控车床坐标系：X=COSα，图4-44，圆的半径R=10，X轴的坐标：X=RCOS（α/n），Z轴的坐标：Z=2πR/n。因此，图4-42、4-43更适合用余弦曲线编程。

谢谢点赞，关注我看更多宏程序编程。