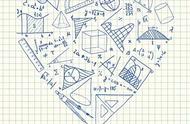
是从 (x,f(x)) 出发的一条割线的斜率, 而且当 h 趋于 0 时, 就成为该点处切线的斜率, 我们所说的含义就在这些接踵而至的陌生概念中丢失了.
事实上, 我们可以从一个描述时刻 的累积量的函数出发, 并问它在 t 时刻的累积率是多少. 厄尔特曼让学生估计一支箭射出 2 秒以后的速度, 假定它在 t 时刻的高度为(图 6.2)


学生们被要求估计这个速度的上界与下界, 并且误差不超过 0.1 米/秒,这使他们能够求出近似速度, 并给出近似值的误差范围.
导数的定义对于理解如何求近似变化率是很重要的. 对于在头一年的微积分课程里关于微分定理的证明, 导数的定义在某种程度上都是本质的.但学生同时要对导数作为瞬时变化率有直观的理解, 即一个物体在给定时刻运动得有多快. 这就对第二章所强调的微分的另一个重要方面——微分方程——提供了自然的引导.
纳入纳皮尔在对数方面的工作的一个原因, 就是要强调他在关联变化率方面的工作. 事实上, 他得到了这样的结果, 若 y 是 x 的对数, 则
其中常数 依赖于对数的底. 不幸的是, 很少有微积分课讲述了微分方程的威力与重要性. 我喜欢麦克斯韦方程组的故事, 因为它诠释了我们如此关心微积分的一个原因, 在用数学模型来揭示这个世界的奥秘方面, 微积分具有难以预料的洞察威力. 许多革新的微积分课程, 包括最早的一些微积分改革课程, 以及我们目前在玛卡莱斯特学院开设的课程, 都是从微分方程开始的, 并且整个课程都在强调微积分可以建立动态模型. 再一次, 软件技术使得学生可以很容易地探究种种模型: 人口增长、流行病的传播、捕食者与被捕食者模型. 这为围绕微积分的学习提供了激动人心的课题. 对如何完成数值近似的分析架起了一座桥梁, 让导数回到变化率的极限.
导数是一个丰富的概念, 带来了众多新的理解. 但对许多学生来说, 他们唯一的收获就是将 x³ 变成 3x², 这是何其不幸!

大多数情况下, 微分约化为求导, 积分约化为求原函数, 无穷级数约化为判定敛散性. 其实无穷级数是关于部分和的一种比较差劲的观点, 因为很少有学生能记住他们曾背诵的收敛判别准则, 我非常赞同许多院校的做法, 先等到学生掌握了作为部分和的泰勒多项式, 然后再分析幂级数的收敛性.á 尽管很有挑战性, 我却乐于纳入拉格朗日余项定理作为控制误差的工具. 这也传递出了中值定理的实际重要性.
我还介绍了欧拉对指数函数的幂级数展开, 展示了无穷和带来的妙趣,我希望我的学生们能够欣赏这个例子. 可以考虑让学生从复利公式