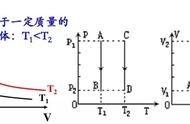
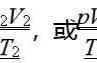一、气体压强的微观意义
从微观的角度看,气体对容器的压强是大量气体分子对容器的碰撞引起的,这就好像密集的雨点打在伞上一样,雨点虽然是一滴一滴地打在伞上,大量密集雨点的撞击,使伞受到持续的作用力。

【演示】
用豆粒做气体分子的模型,可以演示气体压强产生的机理。
把一颗豆粒拿到台秤上方约10cm的位置,放手后使它落在秤盘上,观察秤的指针的摆动情况。再从相同高度把100粒或者更多的豆粒连续地倒在秤盘上(图),观察指针的摆动情况。
使这些豆粒从更高的位置落在秤盘上,观察指针的摆动情况。

从微观角度来看,气体压强的大小跟两个因素有关:一个是气体分子的平均动能,一个是分子的密集程度。
【气体压强的简单推导】
例题:高压采煤水枪出水口的横截面积为S,水的射速为,射到煤层上后,水的速度变为零,若水的密度为ρ,求水对煤层的冲力大小。


以上题为参考,建立一个气柱模型,气体分子速度为v,打在S面持续时间为t=l/v,气体分子打在S上为弹性碰撞,设单位体力内分子数为n₀,一个分子质量为m,则F·t=2n₀lSmv,Fl/v=2n₀lSmv,得F=2n₀Smv²,Ek=mv²/2,F=4n₀SEk,P=F/S=4n₀Ek,考虑气体分子在6个面机会均等,朝一个方向运动的分子数应该占总体的1/6,即n₀/6,P=4n₀Ek/6=2n₀Ek/3
气体的压强P=2n₀Ek/3(Ek为气体分子的平均动能)
一定质量的理想气体压强取决于气体分子数密度和平均动能.
【理想气体气态方程推导】
(1)玻意耳定律(玻-马定律)
当n,T一定时 V,P成反比,即V∝(1/P)①
(2)查理定律
当n,V一定时 P,T成正比,即P∝T ②
(3)盖-吕萨克定律
当n,P一定时 V,T成正比,即V∝T ③
(4)阿伏伽德罗定律
当T,P一定时 V,n成正比,即V∝n ④
由①②③④得
V∝(nT/P) ⑤
将⑤加上比例系数R得
V=(nRT)/p 即PV=nRT
【平均动能取决于温度推导】
PV=nRT,得P=nRT/V,
又P=2n₀Ek/3=nRT/V,
得Ek=3nRT/2n₀V=3nRT/2N
=3nRT/2NA·n=3RT/2NA(NA为阿伏伽德罗常数)
Ek=3kT/2(k为玻尔兹曼常数)
温度是分子平均动能的标志.
二、对气体实验定律的微观解释
用分子动理论可以很好地解释气体的实验定律。
一定质量的某种理想气体,温度保持不变时,分子的平均动能是一定的。在这种情况下,体积减小时,分子的密集程度增大,气体的压强就增大。这就是玻意耳定律的微观解释。一定质量的某种理想气体,体积保持不变时,分子的密集程度保持不变。在这种情况下,温度升高时,分子的平均动能增大,气体的压强就增大。这就是查里定律的微观解释。一定质量的某种理想气体,温度升高时,分子的平均动能增大。只有气体的体积同时增大,使分子的密集程度减小,才能保持压强不变。这就是盖一吕萨克定律的微观解释。
,