※CIt :在某一时点t流入系统的资金称为现金流入;
※COt :在某一时点t流出系统的资金称为现金流出;
※NCF(Net Cash Flow)或CI-CO:同一时间点的现金流入与现金流出之差称为净现金流量。
※现金流入量、现金流出量、净现金流量统称为现金流量。
※现金流入和流出是从研究对象的角度划分的。
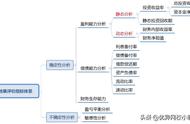
2.现金流量图※现金流量图是一种反应经济系统资金运动状态的图示,运用现金流量图可以形象、直观地表示现金量的三要素:大小(资金数额)、方向(资金流入或流出)和作用点(资金流入或流出的时间点)。
※时点即表示与之相连的前一时间单位结束,又表示后一时间单位的开始。
(二)资金的时间价值1.资金时间价值的含义※资金在运动之,其数量会随着时间的推移而变动,变动的这部分资金就是原有资金的时间价值。
2.利息和利率※利息是资金时间价值的一种重要表现形式,甚至可以用利息代表资金的时间价值。
※通常,用利息作为衡量资金时间价值的绝对尺度,用利率作为衡量资金时间价值的相对尺度。
※I=F-P;I:利息;F:还本付息总额;P:本金。在资金借贷过程中,债务人支付给债权人的超过原借款本金的部分就是利息。
※从投资角度看,利息体现为放弃现期消费的损失所做的必要补偿。
※i=It/p;i:利率;It :一个时间单位内的利息;P:借款本金。
※影响利率的主要因素:①社会平均利润率;②借贷资本供求情况;③借贷风险;④通货膨胀;⑤借款期限。
二、利息计算方法(一)单利计算※利息计算方法有单利(利不生利)和复利(利滚利)之分。
※单利终值系数:(1 n*id);id :计息周期单利利率;P:本金。
※n期末单利本利和F=P In=P(1 n*id),n和id反映的周期要匹配。
(二)复利计息※It=i*Ft-1;It:第t个计息期利息额;i:计息周期复利利率;Ft-1 :第(t-1)个计息期末复利本利和。
※复利计算:间断复利和连续复利。
※第t年末的复利本利和Ft=P*(1 i)n
三、等值计算(一)影响资金等值的因素※影响资金等值的因素:①资金多少;②资金发生时间;③利率(折现率)大小(是一个关键因素,在等值计算中,一般以同一利率为依据);
(二)等值计算方式※等值计算方法主要包括:一次支付和等额支付。
1.一次支付情形※一次支付又称整付,是指所分析系统的现金流量,无论是流入还是流出,只在某一时点上发生一次。
※终值计算(已知P求F);实际意义:现有一笔资金P,计息周期利率为i,按复利计算,则n期末的本利和F为多少?
※一次性支付n期末本利和F=P(1 i)n。
※(1 i)n称为一次性支付终值系数。
※(1 i)-n称为一次性支付现值系数(折现系数、贴现系数)。
※折现、贴现:一般是将未来时刻的资金价值折算为现在时刻的价值。
2.等额支付系列情形※F=A*[(1 i)n-1]/i,等额支付系列终值计算公式。
※[(1 i)n-1]/i等额系列终值系数或年金终值系数,用(F/A,i,n)表示。
※P=A[(1 i)n-1]/i(1 i)n现值计算(已知A求P)。
※[(1 i)n-1]/i(1 i)n称为等额系列现值系数或年金现值系数,用(P/A,i,n)表示。
※A=P*i(1 i)n/[(1 i)n-1],资金回收计算,已知P求A。等额支付系列资金回收计算是等额支付系列现值计算的逆运算。
※i(1 i)n/[(1 i)n-1]称为等额支付系列资金回收系数,用(A/P,i,n)表示。
※A=F*i/[(1 i)n-1];偿债基金计算,已知F求A。
※i/[(1 i)n-1]称为等额支付系列偿债基金系数,用(A/F,i,n)表示。

※从复利系数的结构的等值计算原理可知,等值计算受到折现率、资金流量数额及发生的时间点的影响,因此在工程经济分析中重视以下两点:
①正确选取折现率。②注意现金流量的分布情况。
(三)名义利率和有效利率※利率周期:笔者认为是相应利率所对应的计算周期。
※计息周期:是用于表示计算利息的时间单位。
1.名义利率※名义利率r是指:计息周期利率i乘以一个利率周期内计息周期数m所得的利率周期利率。即:r=i*m。
※计算名义利率时忽略了前面各期利息再生利息的因素,这与单利的计算相同。
※通常所说的利率周期利率都是名义利率。
2.有效利率
※有效利率是指资金在计息中所发生的实际利率,包括计息周期有效利率和利率周期有效利率。
※计息周期有效利率:i=r/m
※利率周期有效利率:ieff=I/p=(1 r/m)m-1
※利率周期有效利率与名义利率的关系实质上与复利和单利的关系相同。
※名义利率r一定时,每年计息期数m越多,ieff与r相差越大,这一结论具有普遍性。因此在工程经济分析中,如果各方案的计息周期不同,就不能简单地使用名义利率来评价。
,