之前分享了一题使用三角形旁心性质巧妙解答求角度难题,收到了很多留言咨询。旁心是三角形五心之中,出场率较低的,所以我们今天来具体介绍一下旁心。
想重温这道求角度的几何题,可以点这里:
三角形旁心及旁切圆性质
旁心有以下性质:
性质1 :三角形的一条内角平分线与其他两个角的外角平分线交于一点,该点即为三角形的旁心。
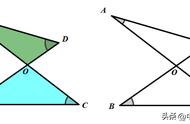
证:如上图,已知角C的外角平分线CD于角B的外角平分线BD交于D,我们来证明AD一定平分角A。
取旁切圆圆D与直线AC和AB的切点,分别为E和F。连接ED、FD,可知角DEA和角DFA均为直角。
ED和DF都是半径,即ED=DF。
三角形ADE与三角形ADF有公共边AD,可得三角形ADE与三角形ADF全等
即可得到角DAF=角DAE,因此,直线AD平分角A。证毕
性质2:旁心到三角形三边的距离相等。
根据角平分线性质,易证此性质
性质3:三角形有三个旁切圆,三个旁心。旁心一定在三角形外。
根据三角形特性,两条三角形外角平分线的交点,一定交于三角形外,易证此性质
性质4:直角三角形斜边上的旁切圆的半径等于三角形周长的一半。

证:如上图,三角形ABC中角A为90度,取BC与圆D的切点为G。
易知三角形DEC与三角形DGC全等,所以EC=CG。同理可知BG=BF。
三角形ABC的周长L=AB AC CB=(AB BG) (AC CG)=(AB BF) (AC EC)=AE AF
四边形AFDE为正方形,AE及AF都等于圆D的半径,得证。
三角形3个旁心组成的三角形为旁心三角形,如下图所示的三角形HDI。这个旁心三角形也有多个美妙的性质。例如:
1)H、C、D三点共线等
2)旁心三角形HDI的垂心是原三角形ABC的内心

此外,其中HB、AD、CI三条线的交点O是三角形ABC的内心,图中红色的圆就是内接圆,与三个旁切圆都相切。
紫色的圆是旁心三角形HDI的外接圆,也称为“贝文圆”。
具体的性质,有兴趣的读者可以自行证明
本自媒体【数学爱好者MathsFans】,长期分享数学趣题、解题技巧,致力于数学科普和拓展数学思维,每日定更,觉得内容有兴趣的可以长期关注哦!
,