初中数学"三线八角”基本图形之中的同位角、内错角、同旁内角的概念是基础之中的基础,既然是基础知识,当然是重要知识,我们不要轻视它,好多同学不能正确认识这三种关系的角,导致后续的学习中走了不少弯路,因为以后的几何学习中时时离不开这三种关系的角,所以一开始就要把它弄清楚,搞明白,下面我们慢慢地辨析它们。
【几个辅助概念】
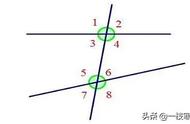
1.三线八角:在同一平面内,任意三条不交于一点的直线中,有两条直线被第三条直线所截构成了八个角,习惯上称为三线八角.如图:

2.截线:需要辨认位置关系的两个角的边所在的公共直线.
3.被截线.两条直线被第三条直线所截,除截线外的另外两条直线.
如上图中,辨认∠4与∠5的位置关系时,∠4与∠5的边所在的公共直线为L,则L称为截线,∠4的另一边在直线a上,∠5的另一边在直线b上,则直线a,直线b称为被截线.
【同位角,内错角,同旁内角的概念】
需要说明的是,同位角,内错角,同旁内角都指的是两个角的位置关系,并不是说哪两个角叫做同位角(或内错角或同旁内角).辨认哪两个角具有上边三种位置关系的某种关系时,首先看这两个角是否能找到截线,若找不到截线,则不具有上述三种位置关系,若找到截线之后再按定义进行辨析.
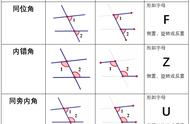
1.同位角:两条直线被第三条直线所截,同时具有下面两个条件时,这两个角才是同位角关系,简称同位角.①两个角位于截线的同侧,②两个角位于被截线的同一方(侧).如图①:

直线AB,直线CD分别与直线EF交于M,N两点,∠1的两条边是ME与MB,∠5的两条边是NM与ND,边ME与边NM共有线为EF,所以EF是截线,而MB在AB上,ND在CD上,所以AB,CD是被截线,∠1与∠5既在截线EF的同右侧,又在被截线AB,CD的同上方,具备两个同上方,同右侧的条件,所以∠1与∠5是同位角关系,习惯上称∠1与∠5是同位角,绝不能认为∠1是同位角,∠5是同位角.图①中∠2与∠6,∠3与∠7,∠4与∠8,也都是同位角.
具有同位角关系的两个角,它们的边构成的图形如同字母"F"形状.如下面四个图中,∠M与∠N是同位角.