对于数学学习的方法我前面的文章有提过。我特别强调的就是基础知识点的理解。比如我们这一章中的相交线所形成的角判断。
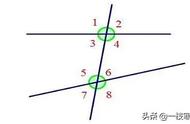
我们的教材当中是这样阐述的,如图所示,直线AB、CD被第三条直线EF所截,构成八个角,简称“三线八角”。

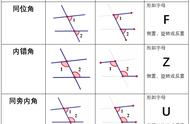
(1),这里的同位角分别是:∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8,他们分别在AB、CD的同侧,而且在EF的同侧。
(2),这里的同旁内角分别是:∠4与∠5,∠3与∠6,他们分别夹在AB、CD之间,而且在EF的同侧。
(3),这里的内错角分别是:∠3与∠5,∠4与∠6,他们分别夹在AB、CD之间,同时又各在EF两侧。
总结:1.不管是哪种角都是成对出现,而且它们的顶点不相同。
2.同位角和同旁内角都有个“同”字,这个“同”是指都在直线EF的同一侧。
3.这三条直线的关系一定要理清楚,直线AB、CD为被截直线,直线EF为截线。这点一定要判断清楚,不管是哪一种角, 他们都有一条边相同或者边的反向延长线相同,也就是我们这里的直线EF。
昨天我讲过数学的分类思想,在复杂图形中识别一个角的同位角、内错角和同旁内角时,经常就要用到这类思想。

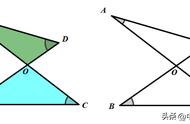
(通过上面的分析,首先我们要找到三线,并且确定哪两条线是被截直线。同时找出第三条截线,也就是我们上面总结当中的公用线。这里我给大家讲一个小技巧:如果这种直线太多的时候,我们可以把需要找的两个角的关系所在的三条直线在草稿纸上面画一遍,这样就和我们例题的情形一样。比如∠A与∠1关系的时候如图所示


解:∠A的同位角有:∠5,∠6,∠7,∠8
∠A的同旁内角有:∠1,∠2,∠3,∠4
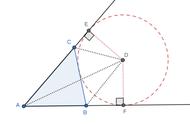
再来做一道容易犯错的题:

(提示:与∠B共边的角有∠BAC和∠BAN哦!)
,