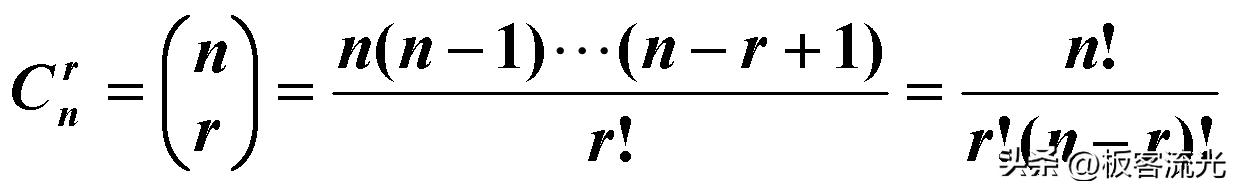概率论与数理统计梳理合集为作者大学自理复习所用
第一章 概率论的基本概念
1.1 随机试验
一、诞生于应用(略)二、随机现象确定性现象:在一定条件下必然发生的事件
随机现象:在一定条件下可能发生也可能不发生,条件与结果之间的关系无法用函数加以描述
三、随机试验(E)定义:(1)相同条件下重复进行(2)可能的结果不止一种,事先明确所有可能结果(3)不确定哪个结果出现
1.2 样本空间与随机事件
一、样本空间(S:所有结果的集合)与样本点(每个结果)二、随机事件(S的子集,用大写字母表示)的概念单点集:基本事件
S:必然事件
∮:(空集)不可能事件
三、随机事件间的关系及运算(一)关系
1.包含:B包含A,A发生B必然发生。
2.和事件:A∪B=A B,A或B至少有一个发生。
3.积事件:A∩B=AB,A发生且B发生
4.差事件:A-B,A发生但B不发生
5.互不相容/互斥:A∩B=空集,A、B不同时发生
*基本事件是两两互不相容的
6.对立事件/互逆事件:A∪B=S,且A∩B=空集,B记作A逆(A上面一横)
*互斥≠对立;互斥不能推出对立,但对立可以推出互斥
(二)运算

1.3 频率与概率
一、频率的定义与性质(略)二、概率的定义与性质性质1:不可能事件的概率为0
性质2:(有限可加性)有限个两两互斥事件的和事件的概率,等于每个事件概率的和
性质3:若B包含A,则P(B-A)=P(B)-P(A),P(B)>P(A)
性质4:对于任意事件A,P(A)≤1
性质5:(逆事件的概率)对任一事件A,A的逆事件的概率等于1-P(A)
性质6:(加法公式)对于任意两事件A,B有P(A∪B)=P(A) P(B)-P(AB)
1.4 等可能概型
一、古典概型定义设E是随机试验,E满足下列条件则称E为等可能概型:
(1)试验的样本空间只包含有限个元素
(2)试验中每个基本事件发生的可能性相同
二、古典概型计算公式
(一)加法原理:完成某件事有两类方法,第一类有n种,第二类有m种,则完成这件事共有n m种方法。
(二)乘法原理:完成某件事有两个步骤,第一步有n种方法,第二步有m种方法,则完成这件事共有nm种方法
(三)排列:
1.有重复排列:在有放回选取中,从n个不同元素中取r个元素进行排列,称为有重复排列,其总数为n的r次方。
2.选排列:在无放回选取中,从n个不同元素中选取r个元素进行排列,称为选排列,其总数为。

选排列公式
(四)组合:
(1)从n个不同元素中取r个元素组成一组,不考虑其顺序,称为组合,其总数为