最近非常想写个关于“四点共圆”的推文。
原因嘛,当然是因为近期一直在复习圆锥曲线,觉得手熟了。
不过最主要的,还是因为最近已有多位同学询问了四点共圆的证明。
好像最近的好几张卷里,也都有四点共圆吧。
翻了翻高考卷,不论是以前的全国卷,还是地方卷,确实出现过多次关于“四点共圆”的证明了。
当然,文科都是压轴的。
于是,我极认真的准备了一点素材,写就此文。
仅希望能给高分段的孩子们,更多一点解析几何题型上的储备吧。
为表示严肃性,还是直接上高考真题吧。
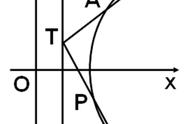
四点共圆-考题再现

这题的第一问,是极其简单的。
因为根据条件,利用向量加法结合韦达定理,就可以直接求出点P的坐标了。
代入就行了呗。

我就不再代入了,直接进行“四点共圆”的证明。
其实,说到四点共圆的证明,记得初中的主要方法,应当是“对角互补的四边形有外接圆”这一结论了。
所以,首当其冲的,要考虑“对角互补”。
只是如何求角呢?
在平面几何里,我们可以用解三角形的办法。
那么,在解析几何里呢?
想了想,也只有“到角公式”和“向量夹角”稍微的靠谱点。

这里,我用了“到角公式”。
只是,要问我什么叫“到角公式”?
我就不再答复你了。
因为画个图仔细想想,很容易就能弄明白的。
当然,有同学说,都把四点坐标求出来了,用向量不也是挺好的嘛。
毕竟,向量求角,我们可能更熟悉点。
但因为要计算模长,可能计算量就稍微显得大了点了。
而且,如果是真的要计算模长的话,我想就无需求角了。
因为圆当中,还有一个非常重要的结论,叫“相交弦定理”!
我们可以用这个定理,成功过渡到“四点共圆”的验证。