这是全国高考数学的真题,它的条件一下子让老黄想到了割线定理。但它却是关于双曲线的,这是怎么回事呢?我们一起来看看题目吧!
设C是双曲线x^2-y^2/16=1的右支,T在直线x=1/2上,过T的两条直线分别交C于A, B两点和P, Q两点,且|TA|·|TB|=|TP|·|TQ|.
求直线AB的斜率与直线PQ的斜率之和.
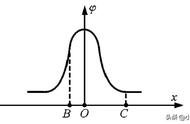
分析:题目本身是没有图的。可以先作出草图帮助理解:

直线AB,PQ显然就是曲线的割线,它们相交于T点,而且|TA|·|TB|=|TP|·|TQ|,这像不像割线定理?在老黄思考这道题的时候,就一直受到这个条件的干扰,希望通过作过A,B,P,Q的圆来解决这个问题,但这样却怎么也走不通。如果大家有兴趣,可以继续走一走,看能不能走得通。好了,言传正传,下面分享这道题的解题过程和思路。
解:如图,设T(1/2,t),则直线AB,和PQ的参量方程分别如下:
{x=1/2 rcosα, y=t rsinα};{x=1/2 rcosβ, y=t rsinβ}, 【α,β分别是直线AP和PQ的倾斜角,接下来求两条直线与双曲线右支的交点情况】
当(1/2 rcosα)^2-(t rsinα)^2/16=1时, (17cos2α-1)r^2 (16cosα-2tsinα)r-(t^2 12)=0.
r1r2=-(t^2 12)/(17(cosα)^2-1)=(a-1/2)(b-1/2)/(cosα)^2,a,b分别为为A,B的横坐标.【式子两端的等量关系是由参量方程化得的】
同理可得:-(t^2 12)/(17(cosβ)^2-1)=(a-1/2)(b-1/2)/(cosβ)^2,p,q为P,Q的横坐标.【由于过程完全一样,只需把α改成β,这里就不做赘述】
由|TA|·|TB|=|TP|·|TQ|, 有(a-1/2)(b-1/2)/(cosα)^2=(p-1/2)(q-1/2)/(cosβ)^2,【这里需要有一转化过程,请自行完成】
所以-(t^2 12)/(17(cosα)^2-1)=-(t^2 12)/(17(cosβ)^2-1),所以(cosα)^2=(cosβ)^2,【根据题目的实际,满足这个条件的α和β只能是互补的关系】
∴tanα=-tanβ, 即AB的斜率与PQ的斜率之和为0.
题目并不十分复杂,但还是比较难的。聪明的您怎么看呢?
,