齐次化方法”解决圆锥曲线中的一类定点问题
定点问题是圆锥曲线中常见的出题形式,是高考命题的一个热点,多以大题的形式出现,也是圆锥曲线问题中的一个难点.化解这类问题的基本思想是函数思想,关键在于引进参数表示直线方程、数量积、比例关系等,根据等式的恒成立、数式变换等寻找不受参数影响的量.
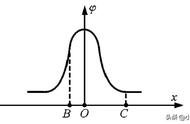
如下图,在定点问题中有一类题是过定点P作两条直线分别交椭圆于A、B两点,若直线PA与直线PB的斜率之积或斜率之和为定值,则直线AB过定点.这种模型可称为“手电筒”模型,解决这类问题采用“齐次化方法”可减少大量计算,达到快速解题的目的.


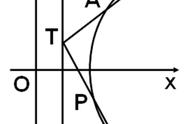
题目分析:这个题目用传统联立的方式做并不难,这里略过,只介绍用齐次化联立的做法.题目中涉及的两条直线OA与OB互相垂直,也即斜率积为-1,其次这两条直线都过原点,因此考虑使用“齐次化方法”.
证明如下: