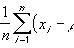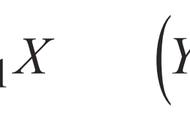这里要区分开观测值和预测值,通过回归方程求得的都是预测值,观察值与预测值的差即为残差,接下来分析三个常见的误差平方和。
依旧以上述广告投入和销售额的关系解释,若没有广告投入这一项,只有销售额,如果按照月份作出销售额的散点图,若想找出一条拟合直线,即让这条直线满足观测值和预测值差e最小,因为没有其他变量,此时的预测值只能是一个常数,即^y=y的平均值,此时观测值与平均值差的平方和记作总平方差。
若引入一个参数,例如广告投入量x,就可以用x的变化来模拟y的变化,原本的预测值就不再是y的平均值,此时^y≠y的平均值,同理若要满足观测值和预测值差e最小,则y-^y最小,而这个平方和叫做残差平方和。
总平方和是什么意思?即没有引入变量时但从销售额角度分析得到的误差平方和;残差平方和是什么意思?即引入变量x后在使用最小二乘法优化之后残留的误差平方和,所以误差平方和减去残差平方和即表示引入变量x之后可以消除的误差,这个差值叫作回归平方和,从上述理解能看到回归平方和的意义是引入x变量消除误差之后剩余的能对自变量解释的部分,即被回归方程解释的部分,因此又叫做解释平方差。
高中阶段的考题更多与残差平方和有关,理解残差平方和与回归平方和的关系即可,深层次内容无需深究。

所以SST-SSE这部分占SST越大,说明引入新变量x之后对误差的减少效应越强,即回归方程的拟合度越好,当这个比值接近1时,说明新加入的x会大大减少预测值的误差,当比值接近于零的时候,说明新加入的x对误差的消除效应几乎为零,可看做回归方程的拟合程度非常差。
因此书上用这个比值变量x对变量y的解释能力,将这个比值命名为判定系数,新课本上改名为可决系数或决定系数,即R²=SSR/SST

因此可知,R²越大,残差平方和越小,被回归方程解释的部分越大,拟合度越好
最后可决系数和相关系数的关系:R²=r²,即可决系数等于相关系数的平方

考试的时候不会让求可决系数,但有可能求相关系数,通过两者的关系即可通过r求可决系数了。
书本上除了一元线性回归方程,还有一元非线性回归方程的求法,其实就多了一步换元,有关一元非线性回归方程的求解可参考链接: