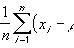作者:Abhijit Telang翻译:张睿毅校对:丁楠雅本文约2600字,建议阅读10分钟。
本文介绍了做残差分析的方法及其重要性,以及利用R语言实现残差分析。
在这篇文章中,我们通过探索残差分析和用R可视化结果,深入研究了R语言。
残差本质上是当一个给定的模型(在文中是线性回归)不完全符合给定的观测值时留下的gap。
医学中的病理学发现的残留分析是一个形象的比喻。人们通常用代谢残留水平来作为衡量药物吸收的指标。
残差是用于建模的原始值与作为模型结果的对于原始值的估计之间的差异。
残差=y-y-hat,其中y是初始值,y-hat是计算值。
期望这个错误尽可能接近于零,并且通过残差找到任何异常值。
找到异常值的一个快速方法是使用标准化残差。第一种方法是简单地求出残差与其标准差的比值,因此,任何超过3个标准差的情况都可以被视为异常值。
## 标准化残差-相对于其标准偏差的比例残差
residueStandard<-rstandard(lmfit)
df[residueStandard>3,]
以下是得到的结果:
days.instant days.atemp days.hum days.windspeed days.casual
442 442 0.505046 0.755833 0.110704 3155
456 456 0.421708 0.738333 0.250617 2301
463 463 0.426129 0.254167 0.274871 3252
470 470 0.487996 0.502917 0.190917 2795
471 471 0.573875 0.507917 0.225129 2846
505 505 0.566908 0.456250 0.083975 3410
512 512 0.642696 0.732500 0.198992 2855
513 513 0.641425 0.697083 0.215171 3283
533 533 0.594708 0.504167 0.166667 2963
624 624 0.585867 0.501667 0.247521 3160
645 645 0.538521 0.664167 0.268025 3031
659 659 0.472842 0.572917 0.117537 2806
当然,我希望我的模型是无偏的,至少我想这样。因此回归线两边的任何残差,如果没有在这条线上,都是随机的,也就是说,没有任何特定的模式。
也就是说,我希望我的剩余误差分布遵循一个普通的正态分布。
使用R语言,只需两行代码就可以优雅地完成这项工作。
- 绘制残差柱状图;
- 添加一个分位数图,其中有一条线穿过,即第一个和第三个分位数。
hist(lmfit$residuals)
qqnorm(lmfit$residuals);qqline(lmfit$residuals)

于是,我们知道这个图偏离了正常值(正常值用直线表示)。
但这种非黑即白的信息一般是不够的。因此,我们应该检查偏态和峰度,以了解分布的分散性。
首先,我们将计算偏态;我们将使用一个简单的高尔顿偏态(Galton’s skewness)公式。
## 分布对称性检验:偏态
summary<-summary(lmfit$residuals)
Q1<-summary[[2]]
Q2<-summary[[3]]
Q3<-summary[[5]]
skewness<-((Q1-Q2) (Q3-Q2))/(Q3-Q1)
skewness
[1] 0.2665384
这量化了分布的方向(分布于右侧或左侧,或者是否完全对称或均匀)。
另一个度量角度是峰度,它显示分布是朝向中心( ve值)还是远离中心(-ve值)。峰度是一个量化离群值可能性的指标。正值表示离群的存在。
kurtosis(lmfit$residuals)
[1] 2.454145
接下来,除了可视化残差的分布,我还想找出残差是否相互关联。
对于一个模型来说,为了解释观测值的所有变化,残差必须随机发生,并且彼此不相关。
Durbin-Watson测试允许检验残差彼此之间的独立性。
dwt(lm(df$days.windspeed~df$days.atemp df$days.hum),method='resample', alternative='two.sided')
lag Autocorrelation D-W Statistic p-value
1 0.2616792 1.475681 0
Alternative hypothesis: rho != 0
对于给定的自由度和观测次数,需要将统计值与临界值表确定的下限和上限进行比较。文中案例的值域是[1.55,1.67]。
由于计算的D-W统计值低于该范围的较低值,我们拒绝了残差不相关的零假设。因此取而代之的假设是残差之间可能存在相关性。
直观地看,这个假设可以通过研究模型在试图捕获原始Y值的增加值时失败的原因来了解。当捕获增加值时,随着y的增加,残差与y成正比。

将其与绘制拟合y-hat值与y值进行比较。当y-hat值趋于落后时,残差似乎与y共同增长,故此,因为过去的残值似乎继续沿着固定的坡度值运行,过去的残值似乎是当前值的更好预测因子。同时,在达尔文-沃森检验(Darwin-Watson tests)中在残差与先前值之间的差的平方和,与所有观测的给定残差之和的比较和对比中,发现了相关性。
因此,残余误差之间的相关性就像心率测试失灵一样。如果你的模型不能跟上Y的快速变化,它会越来越和一个检验玩命的跑步者的情况类似,没记录上的步数似乎比跑步者实际的步数更相关。