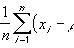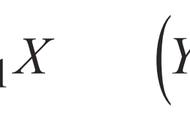重构你的线性回归模型中的下意识影响。
有一点很重要:当对任何给定的观测集进行线性回归时,因变量(符号上表示为y)的计算估计量(符号上表示为y-hat)的每个值不仅依赖于当前值(例如,观察值),还依赖于每次观测。
毕竟,你的多元线性回归模型只在最小化因变量y的实际值和所有观测值y(y-hat)的计算估计值之间的误差后,才计算出每个影响因素的系数。
在数学上,这可以用简单的加权平均模型表示,如下所示。
Yhat(j)= w1j*Y(1) w2j*Y(2) w3j*Y(3) w4j*Y(4) ..... wnj*Y(n);
where n is number of observations and j is one particular estimated value.
如果你想用矩阵表示法来考虑这个问题,矩阵w的维数是[n,n],其中n是观察到的数目。同样,以矩阵形式表示的y具有尺寸[n,1],因此y-hat[j]表示为矩阵,因为它是两个矩阵(w和y)的乘积,并且具有与y相同的尺寸[n,1]。
因此,计算出的估计量的每一个值都可以表示为所有初始y值的加权平均值,表明给定的计算估计量在多大程度上受到每个初始y值的影响。
更简单地说,如果我看到一堆分散的观察结果,我必须以尽可能小的偏差,画一条直线穿过它们,也就是说,如果我必须遗漏一些观察结果,我必须在这条回归线的两侧平等地遗漏。

但是在这样做的同时,我(或选择的回归程序)不管来源何处,下意识地估计了每次观察对我回归线的斜率的影响程度。
我现在所做的就是重新计算这些影响。为了改变我的回归线,将它们包括在内或排除在外,每一个观察值的权重是多少?
权重的统计术语是hat values,因为它们连接了计算的估计量和它们的原始对应的估计量。
以下是用R语言计算的方法:
modelmatrix<-model.matrix(lmfit)
hatvalues<-hat(modelmatrix)
首先,我们得到一个矩阵形式的模型。然后我们计算hat值。
或者,可以使用以下函数获得类似的结果。
hatvalues<-lm.influence(lmfit)$hat
让我们考虑一下可以施加在每个权重上的限制。
显然,权重的最小可能值等于所有原始Y值贡献相等的可能性(因为它们必须为线性回归程序贡献一些东西,通过对所有观测进行工作和优化来估计系数)。
在这种情况下,其值域的下限为1/n,其中n是观测总数。在任何情况下,因为n总是 ve,所以权重总是<1。
现在试着将hat值加和,你会看到一个有趣的结果…
sum(hatvalues)
[1] 4
它们等于线性回归模型为计算考虑的影响因素数量 1。
例如,在示例数据集中,我们有三个因素,即温度、湿度和风速。

接下来,我们如何找到最重要或最有影响的观察结果?
一种优雅的方式是:
- 将hat值切分为四分位数。
- 应用95%标准过滤最异常值。
- 将该过滤标准应用于观察结果。
R语言允许你一步完成这些操作!
df[hatvalues>quantile(hatvalues,0.95),]
我们可以得到满足这一标准的具体观测结果。
days.instant days.atemp days.hum days.windspeed days.casual
9 9 0.1161750 0.434167 0.361950 54
21 21 0.1578330 0.457083 0.353242 75
22 22 0.0790696 0.400000 0.171970 93
26 26 0.2036000 0.862500 0.293850 34
32 32 0.2345300 0.829565 0.053213 47
36 36 0.2430580 0.929167 0.161079 100
45 45 0.3983500 0.375833 0.417908 208
50 50 0.3914040 0.187917 0.507463 532
65 65 0.3662520 0.948261 0.343287 114
69 69 0.3856680 0.000000 0.261877 46
90 90 0.2575750 0.918333 0.217646 179
94 94 0.5429290 0.426250 0.385571 734
95 95 0.3983500 0.642083 0.388067 167
106 106 0.4254920 0.888333 0.340808 121
153 153 0.6439420 0.305000 0.292287 736
239 239 0.6355560 0.850000 0.375617 226
249 249 0.5152000 0.886957 0.343943 204
293 293 0.4665250 0.636250 0.422275 471
302 302 0.2279130 0.882500 0.351371 57
341 341 0.4002460 0.970417 0.266175 50
368 368 0.1262750 0.441250 0.365671 89
383 383 0.2752540 0.443333 0.415429 109
388 388 0.2430580 0.911250 0.110708 145
408 408 0.1016580 0.464583 0.409212 73
421 421 0.2556750 0.395833 0.421642 317
433 433 0.5246040 0.567500 0.441563 486
434 434 0.3970830 0.407083 0.414800 447
463 463 0.4261290 0.254167 0.274871 3252
465 465 0.4766380 0.317500 0.358196 905
478 478 0.3895040 0.835417 0.344546 120
543 543 0.5947040 0.373333 0.347642 1077
627 627 0.5650670 0.872500 0.357587 371
667 667 0.4677710 0.694583 0.398008 998
668 668 0.4394000 0.880000 0.358200 2
694 694 0.2487420 0.404583 0.376871 532
722 722 0.2361130 0.441250 0.407346 205
726 726 0.2203330 0.823333 0.316546 9
最终,你可以用颜色编码使他们具象化。
##具象化
plot(df$days.casual,lmfit$fitted.values,col=ifelse(hatvalues>quantile(hatvalues,0.95),'red','blue'))

就是这样!这是进行残差分析和其重要性的简单概述。
原文标题:
Doing Residual Analysis Post Regression in R
原文链接:
https://dzone.com/articles/doing-residual-analysis-post-regression-in-r
编辑:王菁
校对:龚力
译者简介