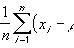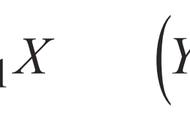多元线性回归分析是当前使用最为成熟、应用最广泛、使用最多的回归分析方法之一。但是很多同学并不能很好的掌握其分析流程,包括多元线性回归的前提条件、软件操作、结果解读等。本文通过一个案例,探讨一下多元线性回归分析流程。
一、多元线性回归方程
多元线性回归是研究多个自变量X对一个因变量Y的影响情况。多元线性回归方程的参数估计方法采用最小二乘法,回归方程的数学模型为:

β0为常数项,又称为截距;βi(i=1,2,...,p)表示除Xi以外的其他自变量固定的情况下,Xi变化一个单位,相应Y的平均变化值,也表示每个自变量对因变量的影响程度。ε为随机误差项,又称残差,是因变量Y的变化中不能用自变量X解释的部分。
二、前提条件
多元线性回归模型的应用需要满足如下前提条件:
①因变量Y为定量数据;
②自变量X个数大于等于2(定量数据和定类数据均可);
③自变量X与因变量Y之间存在线性关系;
④自变量之间不存在多重共线性;
⑤各观测值之间相互独立,即残差之间不存在自相关;
⑥残差服从均值为0,方差为σ^2的正态分布(残差服从正态分布和方差齐)。
条件①②与研究设计有关,条件③-⑥需要使用软件进行验证。
提特别示:当自变量为定类数据时,比如专业(共分为‘理科类’,‘工科类’和‘文科类’)通常需要进行哑变量处理,然后再进行回归分析等。
原因:自变量为定类数据时,不能得到X越如何,Y越如何的结论。进行虚拟变量设置后,定类数据的回归分析才有意义,比如得到“相对于文科类专业(数字0);非文科类专业(1)工资越高”这样的结论。
- 参照项:专业为3类,进行哑变量处理后,在回归模型中,只能放入2个哑变量,因为需要留一个专业作为参照项。比如将文科类作为参照项,后续可以得到“相对于文科类专业,理科or工科类怎样怎样”的结论。并且从数学角度来讲,如果专业对应的3个虚拟变量都放入模型,一定会出现‘多重共线性问题’。
接下来,通过一个案例,介绍如何使用软件进行多元线性回归分析,以及分析结果应该如何解读。
三、案例实战
案例背景:当前有一家公司,想要研究员工的初始工资、工作时间、教育程度、工作经验是否会影响员工的当前工资,如果有影响,各个因素对当前工资的影响大小如何,故通过多元线性回归进行分析。
1前提条件检验
条件③:自变量X与因变量Y之间存在线性关系;
多元线性回归分析要求自变量X与因变量Y之间存在线性关系,可以通过绘制散点图或者查看变量之间的相关系数的方式进行。本案例使用散点图用于直观展示自变量X与因变量Y之间的关系情况,利用SPSSAU可视化->散点图进行分析,操作如下:

SPSSAU输出散点图如下: