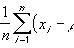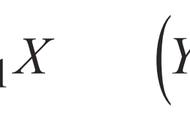从直方图可以判断,基本满足“中间高,两头低”的钟形分布形态,可以认为标准化残差值满足正态分布。
残差方差齐检验
残差的方差齐性,可通过标准化残差值与标准化预测值的散点图来判断方差齐性。以标准化残差为Y轴,标准化预测值为X轴绘制散点图,如果所有点均匀分布在直线Y=0的两侧,则可以认为满足方差齐性,散点图结果如下:

从散点图可以发现数据大致均匀分布在Y=0的两侧,所以可认为残差满足方差齐性。综上所述,数据满足回归分析的前提假设,可以进行多元线性回归。
2多元线性回归分析结果解读
(1)总体显著性检验
多个自变量与因变量这个整体的显著性检验,是使用F检验进行的,可以判断多元线性回归方程是否成立。SPSSAU多元线性回归分析F检验输出结果如下:

从上表可以看出,统计量F=6075.9224,对应的p值小于0.05,所以多元线性回归通过总体显著性检验,回归模型是具有统计学意义的。
接下来查看每个自变量对因变量影响的显著性,即回归系数显著性检验。
(2)回归系数显著性检验
回归系数显著性检验是指每个自变量对因变量影响的显著性检验,使用t检验进行。SPSSAU输出每个自变量对因变量影响的t检验结果如下:

从上表可以看出,初始工资、教育程度与工作经验三个自变量对应t检验的p值均小于0.05,呈现出显著性特征。说明三个自变量X对因变量Y(工资)均有显著影响。
(3)R方与调整后R方
R方用于分析模型的拟合优度,又称决定系数。R方的值介于0~1之间,代表模型的拟合程度,一般认为越大越好。例如R方为0.5,说明自变量可以解释因变量50%的变化原因。但是实际研究中并不会过多关注R方的大小,因为进行回归分析更多的主要关注自变量对因变量是否具有影响关系。调整后R方并没有实际意义,通常在进行模型调整(增加或者减少变量个数时)使用,用于判断你的模型中该不该加入你想加入的变量。