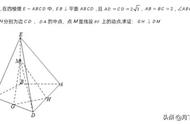
一、证明线面垂直的方法
1,定义法;
2,判定定理法:要着力寻找平面内两条相交直线(有时作辅助线),结合平面图形的性质(如勾股定理逆定理、等腰三角形底边中线等)及一条直线与平行线中一条垂直也与另一条垂直等结论来论证线线垂直。

二、证明空间两条直线垂直的方法
利用线面垂直的判定定理先证明其中一条直线与一个平面垂直,再说明另一条直线在这个平面内即可,这就是常说的“要证线线垂直,先证线面垂直”。

三、求直线与平面所成的角的一般步骤
第一,作:在斜线上选取恰当的点向平面引垂线,在这一步,确定垂足的位置是关键;
第二,证:证明所找到的角为直线与平面所成的角,其证明的主要依据为直线与平面所成角的定义;
第三,求:一般来说是借助解三角形的知识求角。

四、空间中证明两条直线平行的方法
(1)利用线线平行定义证两线无公共点;(2)若 a ⫽ b , b ⫽ c ,则 a ⫽ c (公理4);
(3)利用线面平行的性质定理把证线线平行转化为证线面平行;
(4)若 a垂直α, b垂直α,则a ⫽ b (线面垂直的性质定理)。
,