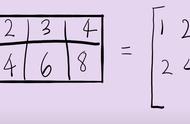
这就是矩阵的分块运算。当然,分块运算还有其他划分形式,读者可参考线性代数的相关内容。如果令y=0,那么式(1.23)就变成了如下形式。
(1.26)
Ax=-6
式(1.26)是一个标准的线性方程组。从矩阵分块运算的角度来看,将n个未知数的m组方程写成了式(1.23)所示的紧凑形式。矩阵可以简化公式的书写。假设.4矩阵是m行n列的,则严格来说还需要Rank (A) =min(m, n)
(1) 如果m=n,那么代表未知数个数与方程个数是相等的,这是一个适定方程。
(2)如果m<n,那么代表未知数个数大于方程个数,这是一个欠定方程。
(3)如果m >n,那么代表未知数个数小于方程个数,这是一个超定方程。
这就有了3种典型问题。对于适定问题,如果矩阵行列式不等于0,那么方程有唯一解(空间中的一个点) ;对于欠定方程,方程具有无穷多个解(一个空间曲面) ;对于超定方程,仅有近似解。机器学习问题应当都是超定问题,也就是方程个数是多于未知数个数的。但是也有些情况例外,比如深度学习模型,未知数个数可能是大于方程个数的。
现在列举一个简单的例子。假设在二维空间中有(1.0, 1.1) (2.0, 1.9) (3.0,3.1) (4.0, 4.0)共4个点,求解这4个点所在的直线。如果直线方程为y=ax b ,那么将4个数据点代入后会得到4个方程,而未知数有a.6两个,因此这就是一个典型的超定问题。此时,对于a、6取得任何值都无法很好地描述通过4个点的直线。但若取a=1,b=0,此时虽然无法精确地描述z和y的关系,但是通过这种方式可以得到(1.0, 1.0),与数据点相比(1.0, 1.1)十分接近,因此得到了近似意义(最小二乘)上的解。这是一个非常典型的机器学习问题。从这个例子可以看到,实际上机器学习就是一个从数据中寻找规律的过程。而假设数据符合直线分布就是我们给定的模型,求解给定模型参数的过程称为优化。这里不需要读者对机器学习问题进行更多的思考,我们在之后还会进行更详细的阐释。这里只是说明机器学习问题大部分情况下是一个超定问题,但由于可训练参数(也就是未知数)较多,在训练样本(每个训练数据都是一个方程)不足的情况下深度学习模型可能并非超定问题,此时会面临过拟合风险,因此对于机器学习尤其是深度学习需要海量(数量远超未知数的个数,未知数也就是可训练参数的个数)的样本才能学习到有价值的知识。
1.2矩阵分解
上面提到空间中某一坐标向量可以写成多个向量相加的形式。
(1.27)

对于一组不全为0的向量而言,如果其中的任意一个向量都不能由其他向量以式(1.27)的方式表示,那就代表这组向量线性无关或这组向量是线性独立的。
线性独立的概念很重要。如果几个向量线性不独立,即某个向量可以用其他向量表示,那么这个向量就没有存储的必要。举个简单的例子。
(1.28)

式(1.28)代表向量

仍是线性相关的,也就是说,我们仅需存储3个向量其中的两个就可以恢复第3个向量。这种恢复是无损的,是信息压缩最原始的思想。这里加强约束,式(1.27)中等式右边各个向量