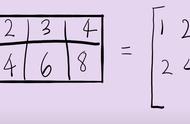
组成的矩阵V可以分解为两个矩阵A,E的乘积表示。如果m >k,也就是说,我们可以用少于m个数字来表示向量V,这是一个标准的数据压缩过程。此时, A可以代表矩阵V的特征,如果要恢复V的话,还需要保存E。但是机器学习中通常只需A即可,因为其带有V的信息。
从前面的内容可以知道,式(1.32)是对矩阵进行的线性变换,这个变换的目的在于信息压缩。这个过程中需要的是求解矩阵E。如果W=E^T,则信息压缩方式可以写为如下形式。

W称为变换矩阵。这是通过矩阵的线性变换来完成数据压缩的过程。
1.3方阵的线性变换:特征值分解
特征值分解是最简单的一种矩阵分解形式,也是矩阵算法中最常用的。特征值分解是对方阵而言的。下面将某个矩阵A分解成3个矩阵相乘的形式。
(1.34)

这是一个矩阵相乘的逆运算,也是一个典型的欠定问题,因为矩阵分解并不是唯一的。为了解决这种非唯一性问题,我们对分解后的矩阵加入约束条件。第一个约束就是特征值分解中E矩阵是正交矩阵。
(1.35)

此时,式(1.33)中的变换矩阵W即为E。另外一个约束就是对角矩阵A ,对角线上的元素称为特征值。E中的向量则称为特征向量。
对于特征值分解而言,其本身具有明确的几何意义。如果将矩阵A当作1.1.2节中的仿射变换矩阵,那么前面提到的坐标与矩阵.4相乘实际上代表了对空间的旋转拉伸变换。由此仿射变换本身可以分解为旋转与拉伸。因此式(1.34)中所得到的矩阵,E代表了对空间的旋转变换, A则代表了对空间的拉伸变换。在此,以二维情况进行简单阐述,如图1.9所示。