图1.9 仿射变换图示
1.4非方阵线性变换:奇异值分解
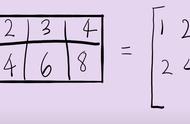
作为矩阵的分解算法,特征值分解最主要的缺陷在于它只能应用于方阵。非方阵情况下的矩阵分解算法,比较有代表性的是奇异值分解(SVD)。
(1.36)

SVD的求解过程可以用特征值分解进行,这就需要将矩阵转换为方阵。
(1.37)

对B进行特征值分解,利用对应元素相等可以得到如下关系。
(1.38)

根据式(1.36)可以得到M的值如下。
(1.39)

图1.9 仿射变换图示
1.4非方阵线性变换:奇异值分解
作为矩阵的分解算法,特征值分解最主要的缺陷在于它只能应用于方阵。非方阵情况下的矩阵分解算法,比较有代表性的是奇异值分解(SVD)。
(1.36)

SVD的求解过程可以用特征值分解进行,这就需要将矩阵转换为方阵。
(1.37)

对B进行特征值分解,利用对应元素相等可以得到如下关系。
(1.38)

根据式(1.36)可以得到M的值如下。
(1.39)













Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.