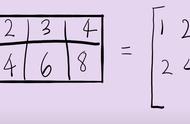
由此3个矩阵已经完全确定。因此,有人说矩阵的特征值分解是SVD的基础。同时可以看到,矩阵A在变换为矩阵M的过程中,相当于对矩阵A进行一次线性变换。
1.5其他线性变换:字典学习
对于SVD分解而言,有一个非常大的问题就是约束过于严格,如矩阵与V为正交矩阵,这就导致在计算的过程中,为了满足分解条件,信息压缩的质量可能会降低。因此,产生了另外一个更加宽泛的约束方式.
(1.40)

假设条件N足够稀疏,此时M就称为字典。在这种情况下弱化了正交性假设,所得到的信息压缩效果会更加出色。
本文节选自《深度学习算法与实践》

本书旨在为读者建立完整的深度学习知识体系。全书内容包含3个部分,第一部分为与深度学习相关的数学基础;第二部分为深度学习的算法基础以及相关实现;第三部分为深度学习的实际应用。通过阅读本书,读者可加深对深度学习算法的理解,并将其应用到实际工作中。 本书适用于对深度学习感兴趣并希望从事相关工作的读者,也可作为高校相关专业的教学参考书。
,