之间的关系如下。
(1.29)

式(1.29)中描述的向量是互相正交的关系,并且是单位向量。
(1.30)

单位向量:长度为1的向量。
向量正交:两个向量内积为0。
坐标基向量是最简单的单位向量。
因此,实际上式(1.27)就是对坐标向量进行的坐标基展开,这是在空间中所用到的概念。当然,并不是所有坐标基向量都是正交的,同样也未必是单位向量。
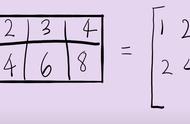
对于一组矩阵的向量

来说,其中的每个向量都可以用其他多个向量以加权求和的方式表示。
(1.31)

之间的关系如下。
(1.29)

式(1.29)中描述的向量是互相正交的关系,并且是单位向量。
(1.30)

单位向量:长度为1的向量。
向量正交:两个向量内积为0。
坐标基向量是最简单的单位向量。
因此,实际上式(1.27)就是对坐标向量进行的坐标基展开,这是在空间中所用到的概念。当然,并不是所有坐标基向量都是正交的,同样也未必是单位向量。
对于一组矩阵的向量

来说,其中的每个向量都可以用其他多个向量以加权求和的方式表示。
(1.31)













Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.