高考力学压轴题的难度通常比较大,综合考查力学概念、力学规律以及物理模型的建立,题目特点往往是物体的运动过程复杂、研究对象比较多,对考生能力的要求较高,通常涉及的知识点有牛顿运动定律、动能定理、机械能守恒定律、动量定理以及动量守恒定律等。有的考生面对如此复杂的试题,会选择“不战而逃”。但实际上如果我们用对方法,从容面对,可能会收到意想不到的效果。
【典例】
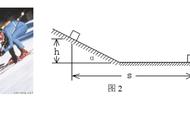
如图所示为某种弹射装置的示意图,该装置由三部分组成,传送带左边是足够长的光滑水平面,一轻质弹簧左端固定,右端连接着质量M=6.0 kg的物块A。装置的中间是水平传送带,它与左右两边的台面等高,并能平滑对接。传送带的皮带轮逆时针匀速转动,速度为v=2.0 m/s。传送带的右边是一半径R=1.25 m、位于竖直平面内的光滑1/4圆弧轨道。质量m=2.0 kg的物块B从1/4圆弧轨道的最高处由静止释放。已知物块B与传送带之间的动摩擦因数μ=0.1,传送带两轴之间的距离l=4.5 m。设物块A、B之间发生的是弹性碰撞,第一次碰撞前,物块A静止。取g=10 m/s2。

(1)求物块B滑到1/4圆弧的最低点C时对轨道的压力;
(2)求物块B与物块A第一次碰撞后弹簧的最大弹性势能;
(3)如果物块A、B每次碰撞后,物块A再回到平衡位置时弹簧都会被立即锁定,而当它们再次碰撞前锁定被解除,求物块B与物块A碰撞的第n次到n 1次之间的过程中,物块B在传送带上运动的时间。
【窍门1】
搜集有用题给信息:物块A的质量M=6.0 kg、传送带的速度v=2.0 m/s、1/4光滑圆弧轨道的半径R=1.25 m、光滑水平面、物块B的质量m=2.0 kg、物块B与传送带之间的动摩擦因数μ=0.1、传送带的长度l=4.5 m。
【窍门2】
分析运动过程,挑选合适的物理规律解题:题目中的第(1)问求解物块B在圆弧最低点时对轨道的压力大小。
物块在圆弧轨道的下滑过程中,由于轨道光滑,在该过程中只有重力做功,则物块在该过程中的机械能守恒,则应根据机械能守恒定律求出物块滑到圆弧底部时的速度;由于该过程物块做圆周运动,求解物块在圆弧底部对轨道的压力时,应通过物块的受力分析找出向心力的来源,再对物块应用牛顿第二定律求出轨道对物块的支持力,然后应用牛顿第三定律求出物块对轨道的压力。
题目的第(2)问求解物块B与物块A第一次碰撞后弹簧的最大弹性势能。物块B滑上传送带后,通过比较物块B的初速度与传送带速度的大小关系分析传送带对物块B的摩擦力方向,进而确定物块B在传送带上的运动过程,结合牛顿第二定律和运动学公式求出物块B离开传送带时的速度,即为两物块碰前物块B的速度;由题意知两物块发生了弹性碰撞,则该过程中两物块的动量守恒、能量守恒,因此应选用动量守恒定律和能量守恒定律列式即可求出碰撞结束瞬间物块A和物块B的速度,紧接着在物块A压缩弹簧的过程中,物块A的动能转化为弹簧的弹性势能,当物块A的速度减为零时,弹簧储存的弹性势能最大,对物块A和弹簧组成的系统由能量守恒定律列式解题。
第(3)问求解物块B在传送带上运动的时间。该过程比较复杂且具有重复性,要通过分析物块B的运动过程,通过计算找出物块B每次在传送带上的运动时间满足的数学规律。
第一次物块B与物块A碰撞结束后,物块B向右运动滑上传送带做减速运动,速度减为零后再向左做加速运动,对该过程可用牛顿运动定律和运动学公式来处理,也可应用动能定理以及动量定理解题;物块B返回传送带左端后,再次与物块A发生碰撞,重复前面的运动过程,通过分析物块B的运动过程,找出碰撞后物块B在传送带上的运动时间遵守的规律,求出时间即可。
解题思路
(1)设物块B沿圆弧轨道下滑到水平位置时的速度大小为v0。
由机械能守恒定律可知:mgR=1/2mv20
解得v0=根号2gR=5 m/s
设物块B滑到圆弧轨道最低点C时受到轨道的支持力大小为F,由牛顿第二定律得:F-mg=mv20/R
解得:F=60 N,方向竖直向上
由牛顿第三定律得:物块B滑到圆弧轨道最低点C时对轨道的压力大小为F′=60 N,方向竖直向下。
(2)因为v0=5 m/s>v,则物块B滑上传送带后开始做匀减速直线运动。设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a,则由牛顿第二定律得:μmg=ma
设物块B通过传送带后运动速度大小为v′,则由运动学公式有v′2-v20=-2al
联立解得:v′=4 m/s
由于v′>v=2 m/s,所以v′=4 m/s即为物块B与物块A第一次碰撞前的速度大小。
设物块A、B第一次碰撞后的速度分别为v2、v1,取向左为正方向。
由动量守恒定律和能量守恒定律得:mv′=mv1 Mv2, 1/2mv′2=1/2mv21 1/2Mv22
解得v1=-1/2v′=-2 m/s, v2=2 m/s
弹簧具有的最大弹性势能等于碰后物块A的初动能:Ep=1/2Mv22=12 J
(3)物块B第一次与物块A碰撞后沿水平台面向右做匀速运动。
设物块B在传送带上向右运动的最大位移为l′,由动能定理得:-μmgl′=0-1/2mv21
解得l′=2 m<4.5 m
所以物块B不能通过传送带运动到圆弧轨道上。当物块B在传送带上向右运动的速度为零后,将会沿传送带向左加速运动。可以判断,物块B运动到左边台面时的速度为v1[KG-*2]′=2 m/s,继而与物块A发生第二次碰撞。设第1次碰撞到第2次碰撞之间,物块B在传送带上运动的时间为t1。则有μmgt1=mv′1-mv1
解得t1=2×1/2×4 s=4 s
设物块A、B第二次碰撞后的速度分别为v4、v3,取向左为正方向,由动量守恒定律和能量守恒定律得: mv′1=mv3 Mv4,1/2mv′21=1/2mv23 1/2Mv24
解得:v3=-1/2×2 m/s=-1 m/s
当物块B在传送带上向右运动的速度为零后,将会沿传送带向左加速运动。可以判断,物块B运动到左边台面时的速度为v′3=1 m/s,继而与物块A发生第3次碰撞。则第2次碰撞到第3次碰撞之间,物块B在传送带运动的时间为t2。
则有:μmgt2=mv′3-mv3
解得:t2=2×1/22×4 s=2 s
同上计算可知:物块B与物块A第三次碰撞和第四次碰撞之间、第四次碰撞与第五次碰撞之间……第n次碰撞与第n 1次碰撞之间物块B在传送带运动的时间分别为t3=1 s、t4=1/2s……tn=1/2n-1×4 s。
即物块B与物块A碰撞的第n次到第n 1次之间,物块B在传送带上运动的时间为tn=1/2n-1×4 s。
【规律总结】
物理压轴题综合性强,涉及的物理过程往往比较复杂,且过程具有多变性, 但复杂多变的物理过程又常常具有阶段性,即包含几个子过程,相对总过程来说,问题通常都要简单得多。因此对于多过程问题,求解的关键是首先按时间和空间上将复杂过程的各个阶段拆分,分析各个子过程的特征,建立正确的物理模型,选用合适的物理规律,然后从各个子过程的运动时间、速度、加速度、位移等方面去寻找它们之间的联系。
今天的内容就先分享到这里,希望能够帮助到各位考生。更多学习方法、学习资料、学业测评、志愿填报方法与技巧,可关注:陕西志愿一点通。
(图文来源:网络)
版权属于原作者或出版商所有,如涉及侵权请联系删除。
,